Coupe pentagonale de la pyramide régulière à base carrée - Définition
En géométrie, il est possible d'opérer une coupe pentagonale régulière de la pyramide régulière à base carrée. Une telle coupe est représentée sur la figure ci-contre.
Problématique
Dans l'espace euclidien, on considère une pyramide régulière (toutes ses arêtes sont de même longueur) à base carrée. Il existe alors un plan dont l'intersection avec la pyramide est un pentagone régulier, c'est-à-dire dont tous les côtés sont de même longueur.
Propriétés de la coupe pentagonale
On note ABCDO la pyramide dont le sommet est O. Le pentagone est noté PQRST où P est situé sur [OC], Q sur [OB], R sur [AB], S sur [AD] et T sur [OD].
Si a est la longueur des arêtes de la pyramide, alors :
- le pentagone a pour côtés (en turquoise sur la figure) :
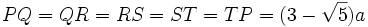
- trois sommets du pentagone (représentés en rouge sur la figure) sont situés à la même distance du sommet de la pyramide le plus proche, à savoir
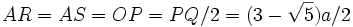
Généralisation de la propriété
Une propriété similaire existe pour la pyramide régulière à base triangulaire, ou tétraèdre régulier, dont une section est un quadrilatère régulier (carré). En revanche, il n'existe pas de coupe hexagonale de la pyramide régulière à base pentagonale.
Plus généralement, si l'on considère une pyramide régulière dont la base est un polygone à n côtés et qu'il existe une section (n + 1)-gonale régulière, alors
- soit n = 3 (tétraèdre) ;
- soit n = 4 (pyramide à base carrée).

















































