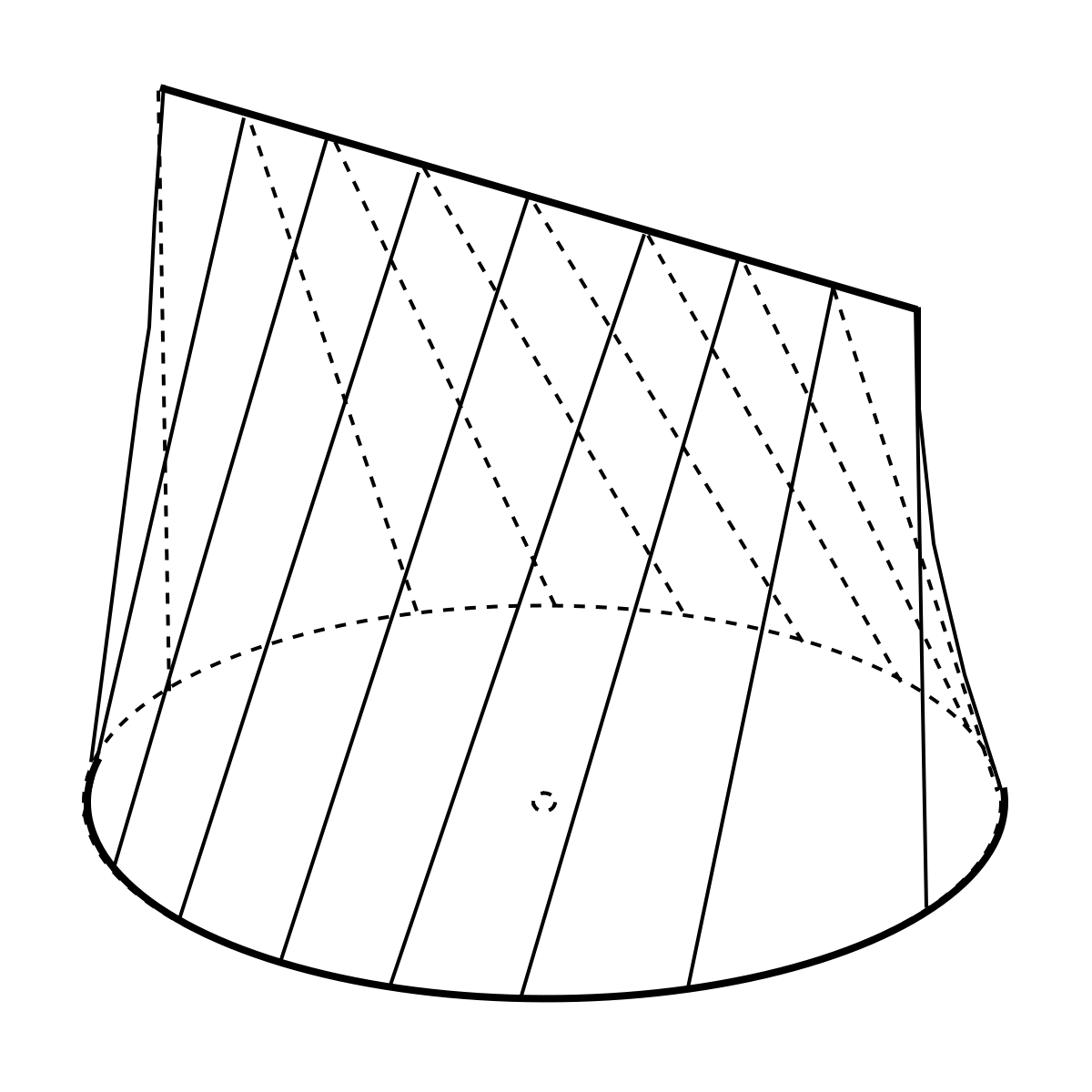
Conoïde - Définition
En géométrie, un conoïde est une surface réglée dont toutes les droites (génératrices) sont parallèles à un plan directeur et passent par une droite (l'axe). Lorsque le plan directeur et l'axe sont perpendiculaires, le conoïde est dit droit.
Un courbe passant par toutes les droites du conoïde est appelée courbe directrice (cela n'inclut évidemment pas l'axe). Pour un plan directeur, un axe et une courbe directrice donnés, il existe une et un seul conoïde.
Le conoïde circulaire droit est le solide engendré par un cercle (C), une droite (d) perpendiculaire à l'axe (Δ) du cercle et des droites s'appuyant sur (C) et (d) perpendiculaires à (d)
Dans le langage courant, on dit d'un objet qu'il est conoïde lorsqu'il a la forme d'un cône. C'est ainsi qu'en anatomie les ligaments conoïdes servent à attacher la clavicule à l'omoplate et les dents conoïdes sont les canines.