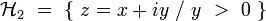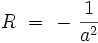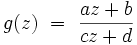Demi-plan de Poincaré - Définition
Le demi-plan de Poincaré est un sous-ensemble des nombres complexes. Il a permis au mathématicien français Henri Poincaré d'éclairer les travaux du Russe Nicolaï Lobatchevski.
Le demi-plan de Poincaré (1882)
Le demi-plan de Poincaré est formé par les nombres complexes de partie imaginaire strictement positive. Il fournit un exemple de géométrie non euclidienne, plus précisement de géométrie hyperbolique.
Géométrie
On considère le demi-plan supérieur :
|
|
Métrique
On munit le demi-plan supérieur de la métrique :
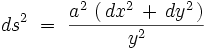
|
Cette métrique possède une courbure scalaire constante négative :
|
|
On se ramène usuellement au cas d'une courbure unité, c’est-à-dire qu'on choisi : a = 1 pour simplifier les équations.
Géodésiques
Les géodésiques sont les demi-droites (au sens euclidien) verticales : x = cte (en rouge) et les demi-cercles (au sens euclidien) perpendiculaires à l'axe des abscisses : y = 0 (en bleu) :
On pourra consulter le site du mathématicien Andrew G. Bennett (université du Kansas) qui contient 3 applets java sur les géodésiques, les cercles hyperboliques et les triangles hyperboliques.
Homographies
Les matrices de
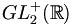
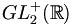
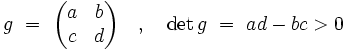
|
Son action sur un point z du demi-plan est donnée par :
|
|
Groupes Fuchiens
Formes automorphes
Dynamique chaotique
Le flot géodésique sur une variété riemannienne à courbure négative est le prototype de système dynamique à temps continu le plus chaotique qui soit, une propriété remarquée dès 1898 par Hadamard [HA98]. On sait aujourd'hui que ce flot est, par ordre croissant d'irrégularités [AA88], [PA91] :
- ergodique
- mélangeant (" mixing ")
- K-système (Anosov)
- C-système = bernouillien [OW73].