Géométrie hyperbolique - Définition

Introduction

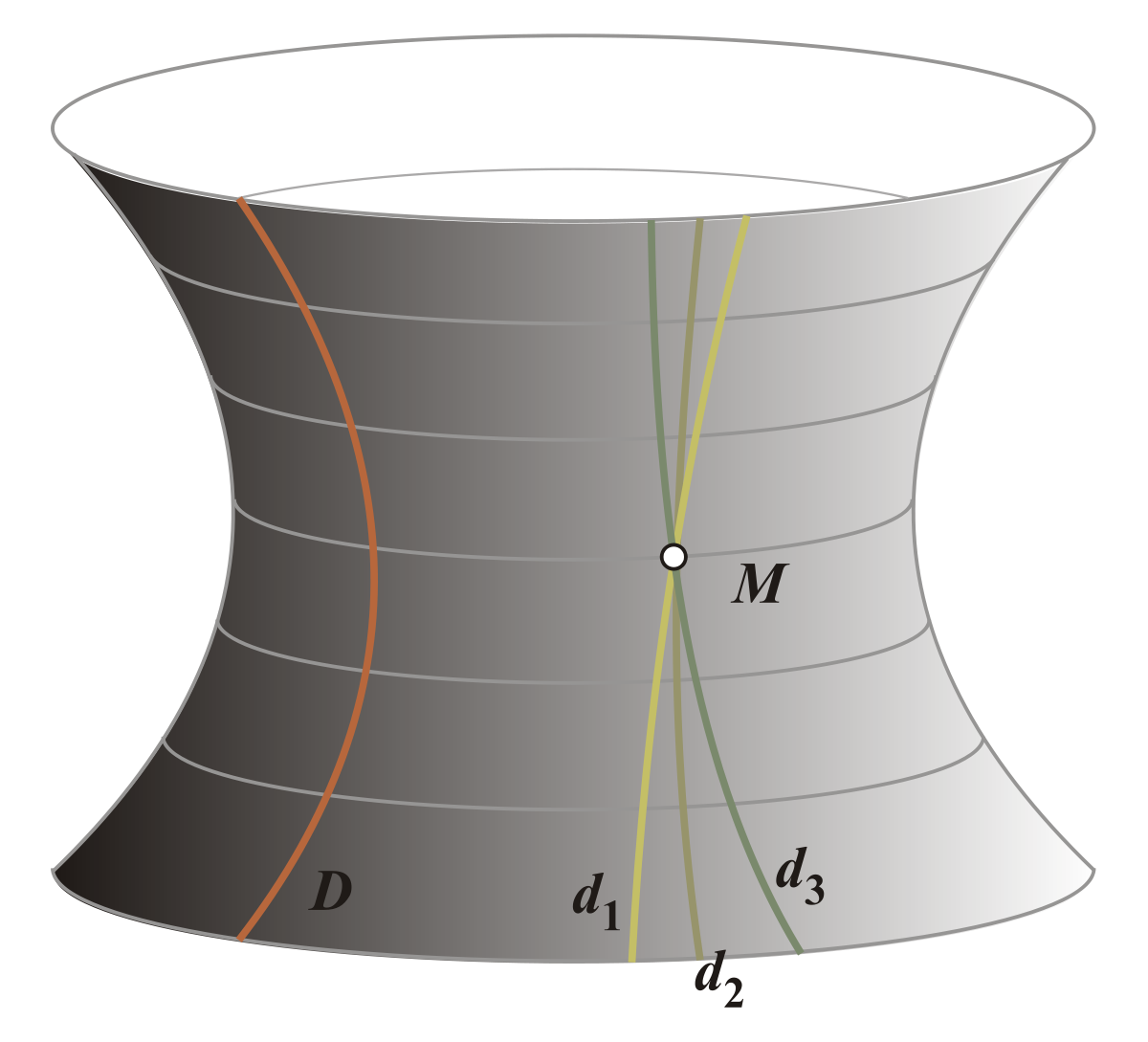
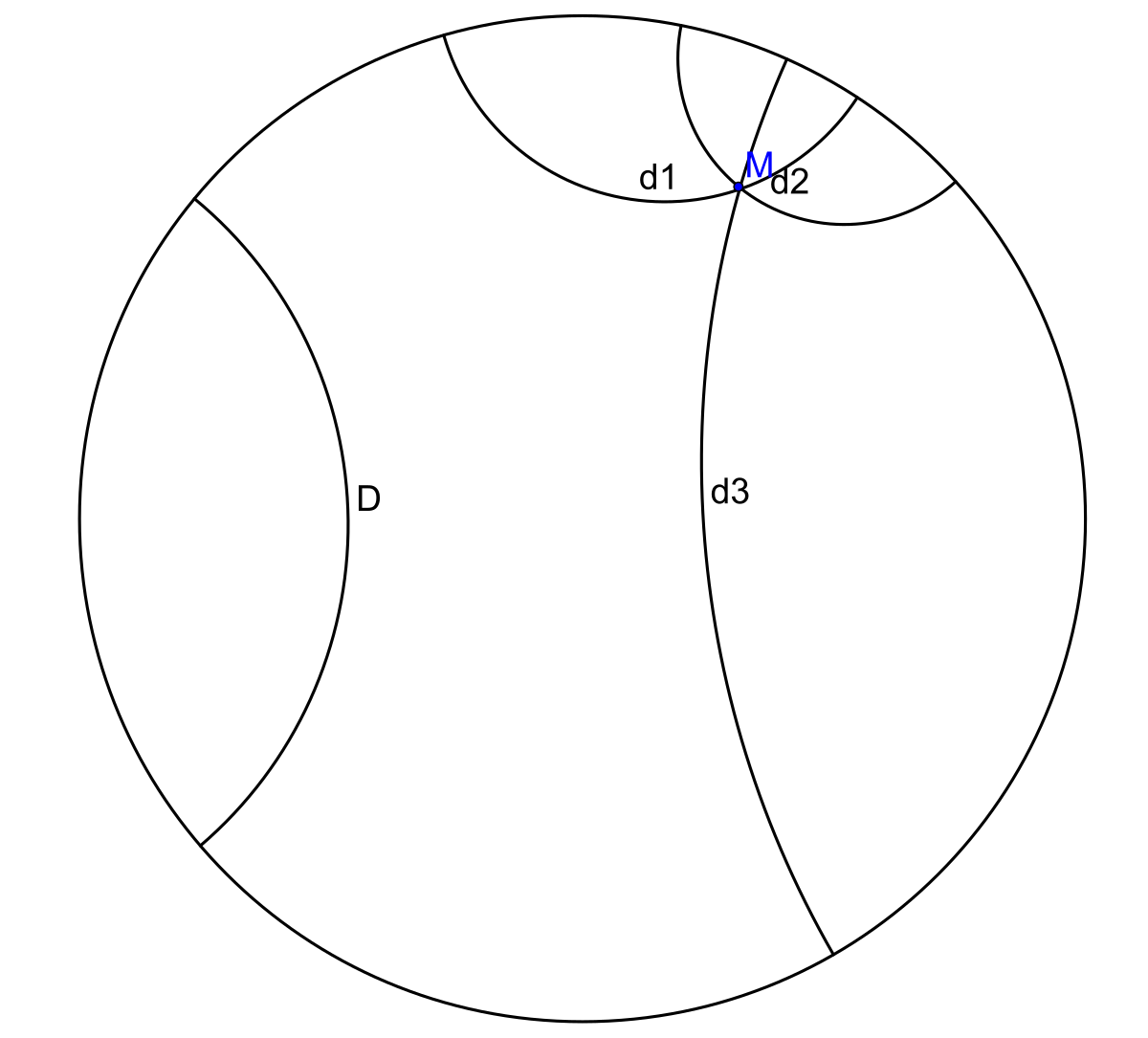
En mathématiques, la géométrie hyperbolique (nommée parfois géométrie de Lobatchevski) est une géométrie non-euclidienne vérifiant les quatre premiers postulats de la géométrie euclidienne, mais pour laquelle le postulat euclidien des parallèles est remplacé par le postulat que « par un point extérieur à une droite passe plus d'une droite parallèle ». On démontre qu'alors il y a une infinité de droites parallèles.

En géométrie hyperbolique, le théorème de Pythagore n'est plus valable et la somme des angles d'un triangle n'est plus égale à π. Une droite est toujours définie comme la ligne de plus court chemin joignant deux points sur une surface.

Lobatchevski, Klein et Poincaré ont créé des modèles de géométrie non euclidienne dans lesquelles on peut tracer une infinité de parallèles à une droite donnée et passant par un même point. On peut citer, en deux dimensions : le disque de Poincaré, le demi-plan de Poincaré, ...

Il existe une infinité de droites qui, comme d1, d2 et d3, passent par le point M et sont parallèles à la droite D (représentation de Lobatchevski)

(représentation de Poincaré)

Historique

L'histoire de la géométrie hyperbolique semble commencer au début du 18e siècle avec les travaux du mathématicien italien Giovanni Girolamo Saccheri, qui chercha à démontrer dans l'œuvre de sa vie, Euclides ab omni naevo vindicatus (Euclide sans erreur), que les postulats d'Euclide étaient cohérents et nécessaires pour définir la géométrie euclidienne. Il chercha notamment, par une démonstration par l'absurde, à obtenir des contradictions en supposant faux le 5e postulat d'Euclide sur les parallèles.

Il échoua dans cette tentative, mais obtint en revanche - en supposant faux le 5e postulat - une grande quantité des théorèmes tout à fait cohérents entre eux, qui appartiennent maintenant à la géométrie hyperbolique. Mais il ne réalisa pas qu'il avait sous les yeux une nouvelle géométrie, et considéra son œuvre et sa vie comme un échec.

Au milieu du 18e siècle, Johann Heinrich Lambert étudia également les conséquences de la négation du 5e postulat d'Euclide, et obtint des théorèmes et des résultats précis appartenant à la géométrie hyperbolique, comme la formule donnant la somme des angles d'un triangle en fonction de sa surface, en géométrie hyperbolique :

CΔ = π − (α + β + γ)

où α,β,γ sont les angles des trois sommets du triangle, C un coefficient de proportionnalité, et Δ la surface du triangle. Vers la fin de sa vie, il semble qu'il ait réalisé que ces théorèmes manifestaient l'existence d'une authentique géométrie "sur une sphère de rayon imaginaire".

Ce sont, près d'un siècle plus tard, les travaux de Carl Friedrich Gauss qui sont généralement reconnus comme étant le véritable point de départ de la géométrie hyperbolique, bien que ceux-ci n'aient jamais été publiés de son vivant. Il formula dans ses notes une théorie structurée, et il semble qu'il avait pleinement conscience que cette géométrie avait un statut mathématique équivalent à celui de la géométrie euclidienne. Il aurait même essayé de mesurer, par des expériences de géodésie, si la géométrie hyperbolique n'était pas à grande échelle la géométrie réelle de l'univers.

Au cours du 19e siècle, la géométrie hyperbolique a été redécouverte et explorée de manière extensive par Nikolaï Lobatchevski en 1830 et indépendamment par János Bolyai en 1832.

Eugenio Beltrami proposa en 1868 plusieurs représentations de la géométrie hyperbolique, dont la représentation conforme et projective, redécouvertes par la suite respectivement par Henri Poincaré et Felix Klein. Il démontra également que si la géométrie euclidienne est mathématiquement cohérente, alors la géométrie hyperbolique l'est aussi nécessairement.