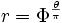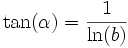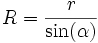Spirale logarithmique - Définition
La spirale logarithmique est la courbe d'équation polaire suivante :
r = abθ
La spirale ci-contre a pour équation polaire :
où

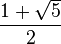
Pour obtenir une spirale symétrique de la précédente par rapport à l'axe (Ox), il suffit de changer b en 1/b.
Fragments d'histoire
La spirale logarithmique porte aussi le nom de spirale équiangle, spirale de croissance

La spirale logarithmique a été étudiée par Descartes et Torricelli qui en a cherché la longueur. Mais celui qui lui a consacré un ouvrage est Jacques Bernoulli qui la nomme Spira mirabilis. Impressionné par ses propriétés d'invariance, il a demandé que soient gravées sur son tombeau à Bâle une spirale logarithmique ainsi que la maxime eadem mutata resurgo (je renais changé à l'identique). Le graveur, plus artiste que mathématicien, a hélas gravé une spirale d'Archimède. D'Arcy Thomson lui consacre un chapitre dans sont traité, On Growth and Form (1917).
Le terme de spirale logarithmique lui est donné par Pierre Varignon.
On retrouve la spirale logarithmique dans la forme de certaines galaxies, dans le developpement de certains coquillages et dans l'agencement de certaines fleurs.
Invariance par similitude
Une rotation de la spirale autour de O d'un angle
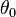
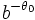
On peut donc remarquer que la spirale logarithmique est invariante par similitude d'angle
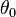
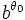
Spirale équiangle
On remarque que la tangente à la courbe au point M fait avec la droite (OM) un angle constant α vérifiant la propriété suivante :
où ln(b) représente le logarithme népérien de b.
Cette propriété est caractéristique des spirales logarithmiques qui sont de ce fait souvent appelées spirales équiangles.
Rayon de courbure
On peut aussi démontrer que le rayon de courbure est directement proportionnel à r selon la loi suivante :
Il est alors facile de trouver le centre du cercle osculateur passant " au plus près " de la spirale au point M. Il suffit de tracer la perpendiculaire à la tangente en M ainsi que la perpendiculaire à (OM) passant par O. Les deux perpendiculaires se coupent en C, centre du cercle osculateur.
La spirale logarithmique de Newton
Ce type de spirale logarithmique possède des applications en dynamique.