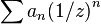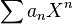Fonction génératrice - Définition

En mathématiques, la fonction génératrice de la suite (a_n) est la série formelle définie par

On confond parfois la fonction génératrice et une fonction de la variable x. Cependant, il est utile de préciser qu'une fonction génératrice est avant tout une série formelle et que la fonction de la variable x correspondante risque de ne pas converger pour tout x.

• fonction génératrice de la suite constante 1 :
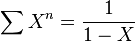
• fonction génératrice de la suite (n) :
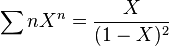
• fonction génératrice de la suite (n²) :
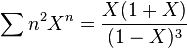
• fonction génératrice de la suite  :

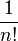
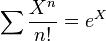
On parle aussi de fonction génératrice exponentielle de la suite (a_n) définie par la série formelle .

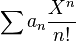
Lorsque l'on travaille plutôt avec l'inverse de X, la variable z=1/X, on parle alors de la transformée en Z , , qui est beaucoup utilisée en traitement du signal et en asservissements.