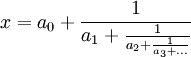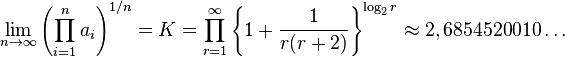Constante de Khintchine - Définition

En théorie des nombres, Alexandre Iakovlevitch Khintchine a démontré que pour presque tous les nombres réels x, l'infinité de dénominateurs du développement de la fraction continuée de x a une propriété surprenante : leur moyenne géométrique est une constante, connue sous le nom constante de Khintchine, qui est indépendante de la valeur de x.

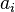
C’est-à-dire, pour

il est presque toujours vrai que

Parmi les nombres x qui ont des développements en fractions continuées qui n'ont pas cette propriété se trouvent les nombres rationnels, les solutions des équations quadratiques à coefficients rationnels (incluant le nombre d'or ), et la base des logarithmes naturels e.

Parmi les nombres qui ont des développements en fractions continuées qui ont apparemment cette propriété (basé sur une évidence numérique) sont , (la constante d'Euler-Mascheroni, et la constante de Khintchine elle-même. Néanmoins ceci est non-démontré, parce que bien que presque tous les nombres réels sont connus pour avoir cette propriété, elle n'a pas été démontrée pour n'importe quel nombre réel précis.

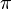
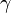
On ne sait pas si la constante de Khintchine est irrationnelle.