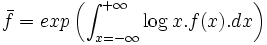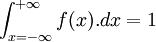Moyenne géométrique - Définition
La moyenne géométrique d'une série statistique quantitative discrète positive non nulle est définie telle que son logarithme est la moyenne arithmétique des logarithmes des valeurs discrètes positives non nulles de la distribution.
Sa formulation mathématique peut se faire comme suit :
-
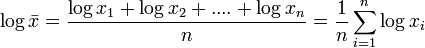
On en déduit :
-
![\bar{x} = \sqrt[n]{x_1 \times x_2 \times .. .. \times x_n} = \sqrt[n]{\prod_{i = 1}^n{x_i}}](https://static.techno-science.net/illustration/Definitions/autres/d/d2c34e03f82648354887195293a79d84_b608305b0831722e5008c4cf696515d4.png)
Pour une série statistique dont le nombre total d’occurrences est infini ou inconnu, mais dont le nombre de valeurs positives non nulles possibles est fini et leurs fréquences respectives dans la série sont connues, la formulation mathématique devient :
-
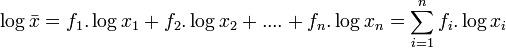
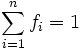
On en déduit :
-
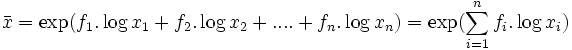
d’où :
-
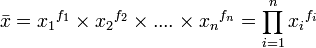
La moyenne géométrique d'une distribution f d'une variable continue à valeur dans un intervalle scalaire fini [x0, x1] est la généralisation à la limite de la formule statistique discrète précédente :
-
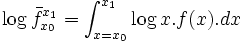
d’où :
-
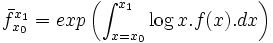
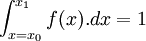
Sa dimension n'est pas une fréquence, mais est celle de sa variable continue.
Si la distribution f est définie sur toutes les valeurs réelles de sa variable continue, la moyenne géométrique de la distribution est :
-