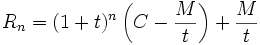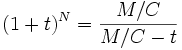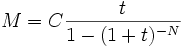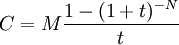Plan de remboursement - Définition

En mathématiques financières élémentaires, un plan de remboursement détermine, lors d'un emprunt à mensualités constantes, les relations existant entre le capital emprunté, le taux d'intérêt, le montant des remboursements et la durée de l'emprunt.

Mise en place mathématique

Un capital C emprunté à un taux mensuel t et remboursé par mensualités constantes M conduit à la construction d'une suite arithmético-géométrique. Si R_n représente le capital restant dû au bout de n mensualités, la suite est définie par la relation de récurrence :

.

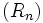
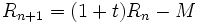
En effet, comme toute dette, durant un mois, le capital R_n va augmenter de si t est le taux d'intérêt mensuel. Comme, au bout d'un mois, il intervient un remboursement d'un montant M, le capital restant dû à l'issue du n + 1^e mois est donc R_{n + 1} = R_n + tR_n − M.

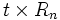
Une première remarque de bon sens consiste à dire que les mensualités doivent être supérieures à donc en particulier à t × C, pour avoir une chance de voir la dette diminuer.

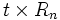
Variables

• C Capital emprunté
• t taux de la période
• M montant de l'échéance
• n nombre d'échéances

Les formules

Une étude de la suite arithmético-géométrique permet de donner R_n en fonction de C, M, n et t.

Comme le but final est de rembourser la somme au bout de N mensualités, la relation existant entre C, M, t et N est donc:

Nombre d'échéances

On peut en déduire, en fonction de M/C et t, le nombre de mensualités nécessaires:

.

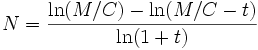
Exemple: si on emprunte 1000 euros à 0,5% d'intérêts mensuels (approximativement 6% d'intérêts annuels) et que l'on rembourse 10 euros par mois, il faut

mensualités .

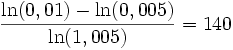
Soit 11 ans et 8 mois.

Montant de l'échéance

On peut aussi déterminer, en fonction de la durée de l'emprunt, le montant des mensualités:

On préfère souvent parler en nombre d'années A et en taux annuel i. Pour des taux faibles (voir suite géométrique), on peut utiliser l'approximation suivante t = i / 12 et on obtient alors la formule suivante

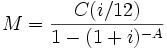
Exemple une somme de 1000 euros, empruntée sur 10 ans, à un taux annuel de 4,8% nécessite un remboursement mensuel de

euros.

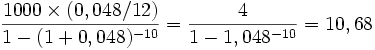
Capital emprunté

Il est possible de déterminer le montant du capital emprunté en fonction de la durée de l'emprunt, du taux et du montant des échéances:

On peut enfin déterminer la somme réellement remboursée, en fonction de la somme empruntée C, de la durée de l'emprunt A et du taux d'intérêt i.

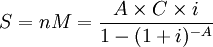
Dans l'exemple précédent, la somme réellement remboursée est de 1282 euros

Tableau de remboursement

Quand sont décidés la somme empruntée, le taux d'intérêt et la durée du prêt, le montant des mensualités est alors fixé. On présente alors un tableau qui précise, mois par mois, le capital restant dû et la part, dans le remboursement, du remboursement des intérêts et de l'amortissement. Ce tableau permet de connaître à tout instant l'état de son compte et la somme à payer en cas de remboursement anticipé.

Exemple : Somme empruntée 1000 euros, durée du prêt 10 ans, taux d'intérêt 4,8%, taux mensuel 0,4%. Tableau de remboursement sur les deux premières années réalisé sur un tableur.

Légende

LxCy = xième Ligne et yième colonne

L(-1) = Ligne précédente

C(-1) = Colonne précédente

Erratum

Dans la formule de la colonne 2 et la ligne 3, L3C6 devrait être L3C7. La formule correcte est donc L(-1)C*(1+L3C7)-L2C7