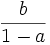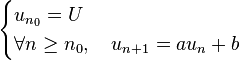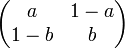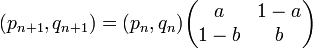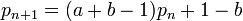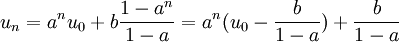Suite arithmético-géométrique - Définition

Une suite arithmético-géométrique est une suite à valeurs dans un corps et définie par récurrence par

En règle générale, on travaille sur (corps des réels) ou (corps des complexes).

Utilisation

La suite arihmético-géométrique se rencontre dans la modélisation de certains flux de population (apport fixe et fuite proportionnelle ): apport de 10 et fuite de 5%,

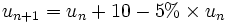
Elle se rencontre aussi dans les plans de remboursement : un capital C emprunté à un taux mensuel t et remboursé par mensualités M conduit à l'élaboration d'un plan de remboursement . Si R_n représente le capital restant dû au bout de n mensualités, la suite est une suite arithmético-géométrique de relation de récurrence : R_{n + 1} = (1 + t)R_n − M

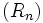
On la trouve aussi dans une chaîne de Markov à deux états . La matrice stochastique est alors

De la relation

On déduit que:

.

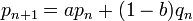
Comme d'autre part,

,

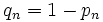
en remplaçant on obtient

Terme général

Pour le cas trivial où a = 1, on a affaire à une suite arithmétique.

Dans le cas où , on cherche par translation à se ramener à une suite géométrique :

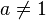
On pose v_n = u_n + c

On démontre que est géométrique ssi

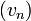
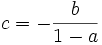
On trouve alors que

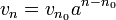
Puis, grâce aux relations entre u_n et v_n,

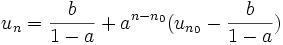
On peut aussi retrouver le terme général, en observant que cette suite consiste à construire la somme des terme d'une suite géométrique. Pour l'illustrer, on peut s'intéresser au cas de la suite définie de la manière suivante (définition 2):

,

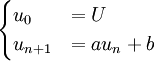
On remarque alors que

u₁ = aU + b

u₂ = a²U + ab + b

u₃ = a³U + a²b + ab + b

Le terme général s'exprime par

.

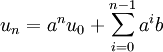
Avec la somme des premiers termes d'une suite géométrique, on obtient le terme général suivant:

En posant , on trouve

.

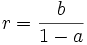
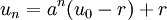
Somme des n premiers termes

Pour une suite définie suivant la définition 2, on a .

Convergence

Le terme général et les considérations sur les suites géométriques permettent de déterminer la limite d'une telle suite suivant les valeurs de a et, éventuellement, le signe de .

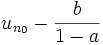
Une remarque intéressante est à faire dans le cas où |a| < 1. Dans ce cas, la limite de la suite est quelle que soit la valeur initiale. La limite d'une suite de ce type est donc complètement indépendante des conditions initiales. Cette particularité est à mettre en regard avec les suites à récurrence non linéaire (fonction logistique) qui peuvent, elles, être très sensibles aux conditions initiales. Dans une chaîne de Markov, cela prouve que la chaîne converge vers une chaîne stationnaire.