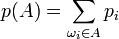Création d'une probabilité - Définition
Cet article fait partie de la série Mathématiques élémentaires |
| Algèbre |
| Analyse |
| Arithmétique |
| Géométrie |
| Logique |
| Probabilité |
| Statistique |
Une expérience aléatoire a conduit à construire un univers Ω formé d'éventualités et à définir des événements (Vocabulaire élémentaire des probabilités). Il s'agit maintenant de quantifier la probabilité de réalisation de chaque événement.
Probabilité sur un ensemble fini
Loi de probabilité
Définir une probabilité sur un ensemble fini c'est affecter à chaque éventualité ωi un réel piqui correspondra à sa probabilité d'apparition. Les seules conditions sur les pi sont les suivantes:
- pi est toujours un réel positif
-
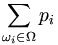
On peut remarquer que les pi sont donc nécessairement des réels compris entre 0 et 1.
La probabilité de l'événement A sera alors
Modèle probabiliste
Il faut être bien conscient que le choix des pi est arbitraire. Le choix que l'on fait est en partie dicté par des a-priori.
Il peut sembler adéquat d'imaginer dans un lancer de dé que tous les numéros ont la même probabilité d'apparaître, les probabilités pi sont alors toutes égales à 1/6. On dit alors que l'on a défini une équiprobabilité sur l'univers {1 ; 2 ; 3 ; 4 ; 5 ; 6}.
Mais il peut tout aussi bien sembler adéquat de considérer que le dé est déséquilibré de telle sorte que la probabilité d'apparition d'un numéro est inversement proportionnelle à celui-ci. Ce qui mène alors à définir la probabilité de la manière suivante:
-
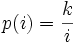
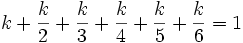
Condition qui conduit à
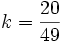
Les deux modèles sont aussi légitimes et correspondent à des réalités différentes. On peut aussi chercher à valider un modèle par l'expérience: la loi des grands nombres stipulant qu'en renouvelant un grand nombre de fois l'expérience, la fréquence d'apparition de l'éventualité ωi est proche de sa probabilité d'apparition, la méthode consiste à renouveler un grand nombre de fois l'expérience et à prendre comme modèle de probabilité les fréquences observées (statistiques inférentielles)
Propriétés des probabilités
-
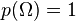
-
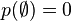
-
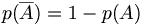
- Si A et B sont deux événements incompatibles (d'intersection vide),
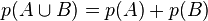
- Dans le cas général,
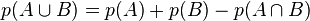
Probabilité sur un ensemble non fini
La construction d'une probabilité sur un ensemble non fini dépasse le cadre des mathématiques élémentaires et fait alors intervenir les axiomes des probabilités. Mais on retrouve le même questionnement sur la validité du modèle et les mêmes propriétés des probabilités.