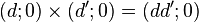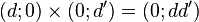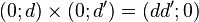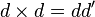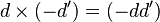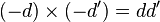Construction des entiers relatifs - Définition

Le but de cet article est de:

• construire comme un ensemble,
• construire une structure de groupe sur cet ensemble,
• montrer que cela prolonge le monoïde (additif) des entiers naturels,

La structure d'anneau sera juste esquissée.

Construction de l'ensemble Z

On sait déjà que l'ensemble des entiers naturels , muni de l'opération interne addition, est un monoïde commutatif; donc notre but est simplement de rajouter un opposé (inverse pour l'addition) pour chaque entier non nul. Il ne s'agit pas de rajouter brutalement un élément, il faut aussi se donner les moyens de définir l'addition sans douleur!

C'est pourquoi on va partir de la notion naïve d'entier relatif, que l'on suppose déjà connue, pour construire l'objet mathématique correspondant. Si on veut définir − 2 avec des entiers naturels, on a envie de le voir comme 0 − 2, ou comme 5 − 7, ou ... ; bref, on a envie de le voir comme la différence de deux entiers naturels. Cela pose une difficulté, car on voit d'une part que l'écriture n'est pas unique, et d'autre part, que cela fait intervenir une opération, la soustraction, qui n'a aucun sens avec les entiers naturels!

On va donc considérer des paires d'entiers, de la forme (n₁,n₂), et considérer que la paire (n₁,n₂) correspond à l'entier relatif naïf n₁ − n₂; et comme on a vu qu'il n'est pas raisonnable de prendre comme ensemble des entiers relatifs, on va regrouper les paires qui correspondent au même entier relatif naïf.

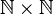
Pour cela, on va définir sur une relation d'équivalence R, par la relation suivante: . Notez qu'intuitivement on est en train d'écrire que deux couples sont égaux si quand on soustrait le second de la paire au premier on obtient le même entier relatif! Mais on n'utilise que la somme pour définir R, donc cette définition n'utilise pas d'objet naïf.

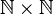
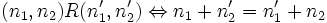
Les relations d'équivalences sont faites pour quotienter; on définit donc:

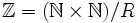
Définition de la structure de groupe

On dispose maintenant de l'ensemble des entiers relatifs; il reste à définir l'addition sur ces derniers: pour cela, on ne dispose que de la définition sur les entiers; on va donc d'abord définir une opération sur les paires d'entiers, et comme elle sera compatible avec la relation R, elle donnera une opération sur les entiers relatifs!

On définit la somme de deux paires d'entier ainsi: (n₁,n₂) + (n₁',n₂') = (n₁ + n₁',n₂ + n₂'); cette opération est visiblement déjà commutative, associative et d'élément neutre (0,0) sur les paires d'entiers; elle passe clairement au quotient, pour donner sur une structure de monoïde commutative.

Il ne reste donc qu'à trouver un opposé à tout entier relatif; mais ceci est immédiat: si (n₁,n₂) représente un entier relatif dans les paires d'entiers, on a (n₁,n₂) + (n₂,n₁) = (n₁ + n₂,n₁ + n₂) où (n₁ + n₂,n₁ + n₂) est équivalent à (0,0), donc la classe d'équivalence de (n₂,n₁) est opposée à la classe d'équivalence de (n₁,n₂)...

Vérification du prolongement

On va montrer qu'il y a un morphisme de monoïdes injectif de dans ; de cette façon, on pourra voir un entier naturel comme un cas particulier d'entier relatif. À nouveau, c'est l'idée naïve que l'on se faisait des entiers relatifs qui montre la voie.

Soit n un entier naturel; on lui associe la classe de la paire (n,0). On voit alors que:

• 0 a pour image la classe de (0,0), donc le 0 des entiers relatifs;
• n + n', la somme de deux entiers, a pour image la classe de (n + n',0), qui est la somme des classes de (n,0) et (n',0).

par ailleurs, on voit bien que cette application est injective, puisque demander que les classes de (n,0) et (n',0) soient égales, c'est justement demander que n = n'!

Écriture simplifiée des éléments de Z

Tout couple d'entiers naturels (n ; m) se trouve dans l'un de ces trois types de classes

• une classe (d ; 0) si n > m avec n = m + d et d non nul
• une classe (0 ; d) si n < m avec n + d = m et d non nul
• la classe (0 ; 0) si n = m

Or l'ensemble des classes (d ; 0) est isomorphe à , on note donc ces classes sous la forme simplifiée d.

D'autre part, pour d non nul, les classes (d ; 0) et (0 ; d) sont opposées. En effet, (d ; 0) + (0 ; d) = (d ; d) = (0 ; 0) en terme de classes. On note donc les classes (0 ; d) sous la forme simplifiée (- d).

L'ensemble retrouve alors sa forme plus classique de .

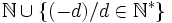
Définition de la multiplication

On peut alors définir la multiplication comme suit: (toujours en s'inspirant de l'analogie avec les entiers relatifs naïfs).

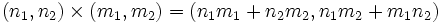
Cette opération définie sur est associative, commutative, possède un élément neutre (1 ; 0) et est distributive pour l'addition précédemment établie. De plus elle est compatible avec la relation d'équivalence. Par passage au quotient, elle confère à une structure d'anneau unitaire.

Les égalités

permettent les écritures

Cette écriture permet de prouver que l'anneau est aussi intègre.