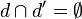Intersection (mathématiques) - Définition
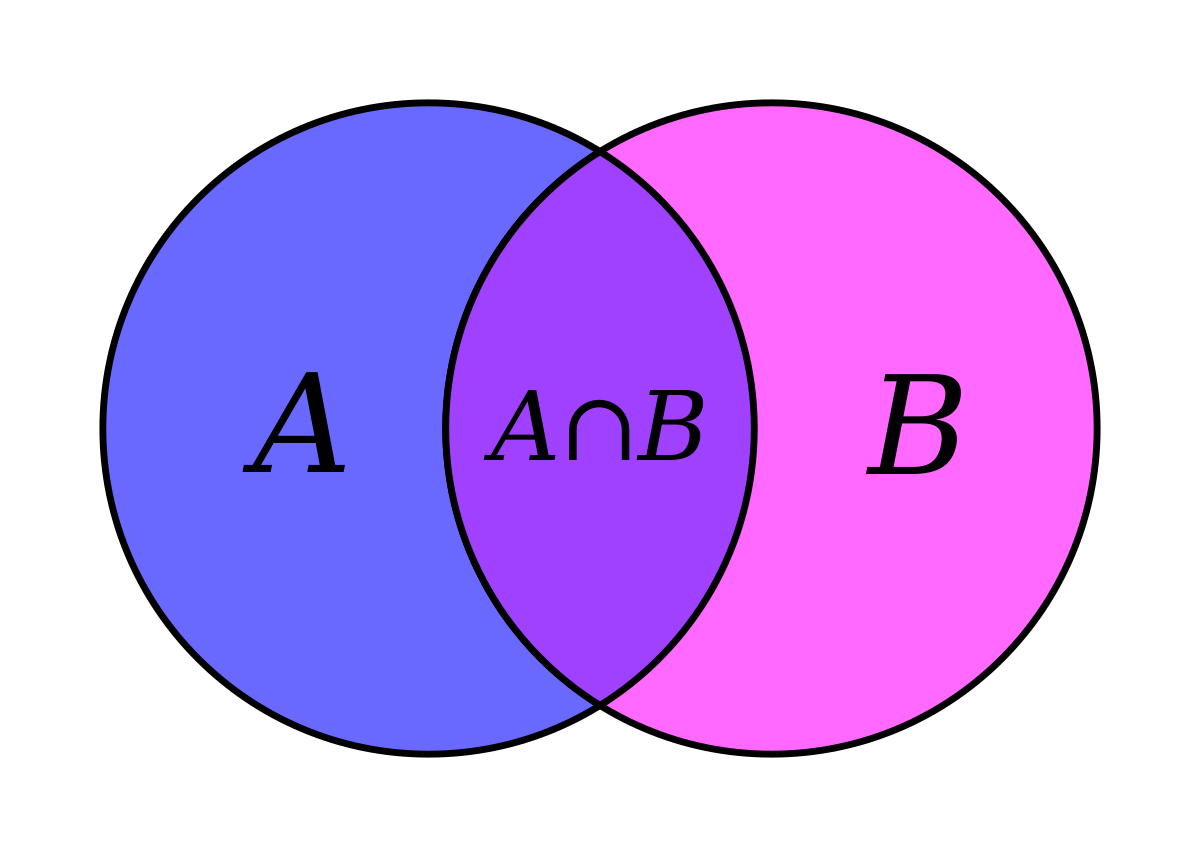
Dans la théorie des ensembles, l'intersection de deux ensembles A et B est l'ensemble qui contient tous les éléments qui appartiennent à la fois à A et à B, et seulement ceux-là.
L'intersection de A et B est notée A∩B.
En algèbre booléenne, l'intersection est associée à l'opérateur logique et.
Géométrie
En géométrie :
- l'intersection de une droite et un plan non parallèles est un point ;
- l'intersection de deux plans non parallèles est une droite.
En géométrie analytique, le système d'équation de l'intersection de deux objets est la réunion des équations de chaque objet.
Intersection de deux droites
Dans le plan
Dans le plan, l'intersection de deux droites, n'étant ni parallèles ni confondues, est un point.
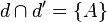
Si les deux droites sont strictement parallèles, il n'y a pas de point d'intersection.
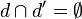
Si les deux droites sont confondues, l'intersection est une droite.
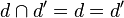
Dans l'espace
Dans l'espace, si deux droites sont coplanaires, on retrouve les mêmes possibilités que dans le plan. Si deux droites sont non-coplanaires, alors elles n'ont aucune intersection.