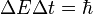Effet tunnel résonnant - Définition
L'effet tunnel est connu comme d'effet inexplicable avec la mécanique classique. Une particule d'énergie inférieure à la hauteur de la barrière possède une probabilité très faible, mais non nulle, de passer au travers.
Un phénomène spectaculaire apparaît dans le cas où la barrière possède, dans sa partie tunnel, un ou des états localisés dont l'énergie correspond à celle de la particule incidente. Un tel état localisé peut être un état atomique d'une impureté, ou au contraire un niveau discret d'un puits quantique créé.
À supposer que par un processus quelconque l'état discret soit occupé à un instant donné, la probabilité pour qu'il se dépeuple vers les états accessibles à l'extérieur de la barrière va provoquer le dépeuplement par effet tunnel à travers les barrières qui le bordent (le niveau n'est donc que quasi-lié). C'est la source de la durée de vie, et de la largeur du niveau du puits. Au niveau de la description, c'est un effet semblable à celui qui est responsable de la largeur naturelle des raies d'émission des atomes.
L'effet tunnel résonnant apparaît lorsqu'un tel système quantique est abordé de l'extérieur avec une énergie proche, ou égale à celle du niveau quasi-lié. La probabilité de passage à travers chacune des barrières d'entrée ou de sortie seule est très faible mais la résonance avec le niveau du puits va piéger la particule quantique, pendant un temps relativement long, de l'ordre de grandeur de la durée de vie du niveau quasi-lié, mais ce piégeage va permettre à la particule de traverser l'ensemble. La transmittivité de la barrière peut approcher l'unité, même pour des barrières épaisses.
On peut noter que plusieurs barrières résonnantes peuvent se suivre, faisant apparaître des bandes de transmittivité importante.
exemple
Prenons comme modèle simple deux barrières de potentiel rectangulaires distantes de quelques nm. Au cas où la hauteur de la barrière serait infinie, le calcul des niveaux discrets serait très simple ; la finitude en hauteur, et l'extension finie à droite, et à gauche ici provoquent un déplacement des niveaux, vers le bas, et l'apparition d'une largeur de niveau (ou autrement dit, d'une durée de vie).
La figure ci-contre montre la transmittivité de la barrière, obtenue par un balayage en énergie. La courbe épouse la forme caractéristique des lorentziennes, propre aux résonances. La mise en évidence des aspects temporels peut s'observer si l'on suit un paquet d'ondes, associé à une particule incidente, venant de la gauche, dont le spectre en énergie recouvre la courbe de résonance.
On observe que la fonction d'onde est en grande partie transmise, qu'elle est considérablement déformée par rapport au paquet entrant, et qu'elle est en retard sur un paquet qui n'aurait pas eu à franchir la barrière. À l'instant où est calculée la fonction d'onde le puits central est encore peuplé : il se vide peu à peu vers les deux demi-espaces libres. Le retard entre les sommet du paquet " libre " et de la partie transmise correspond à la durée de vie Δt du niveau quasi-libre, soit :
-