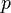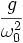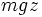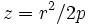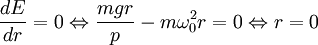Pendule de Huygens - Définition

En physique, le dispositif appelé pendule de Huygens, en l'honneur du physicien Christiaan Huygens, est constitué d'un point matériel M, pesant, se déplaçant sur une parabole d'équation , dans un plan tournant à la vitesse angulaire , d'axe vertical.

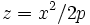
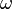
Il ne mérite de fait pas son appellation de " pendule " puisqu'il n'oscille pas. Néanmoins il fournit un résultat intéressant pour la compréhension du pendule conique.

Présentation

Huygens a imaginé une came d'équation :

,

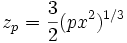
c'est-à-dire l'équation de la développée de la parabole.

On constate que si le point dépasse une certaine vitesse angulaire critique, donnée par :

il se retrouve soit en bas, soit en haut du dispositif. Le cas d'équilibre indifférent est atteint quand la vitesse angulaire de son déplacement est égale à cette vitesse critique.

Explications

On considère les énergies potentielles des forces en présence dans le référentiel tournant :

• l'énergie potentielle de pesanteur , avec , soit

 ;

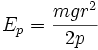
• l'énergie potentielle dont dérive la force d'entraînement (axifuge, ou " centrifuge ") :

.

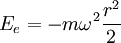
Le mobile M se situe, à l'équilibre, au point où l'énergie totale atteint un extrémum, c'est-à-dire au point où sa dérivée s'annule :

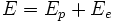
C'est-à-dire lorsque :

.

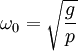
Lorsque , M se trouve en bas de la parabole. Lorsque toute la parabole se trouve à l'équilibre, M reste immobile, là où il se trouvait lorsque la vitesse critique a été atteinte. Le cas où M se trouve en haut est un cas hors équilibre, dû aux contraintes physiques posées par la came.

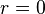
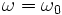
Observation

On peut observer la parabole de Huygens avec un liquide :

• on emprisonne de l'eau colorée entre deux plans transparent verticaux et très proches, pour obtenir un film de liquide (qui ne remplit pas entièrement l'espace entre les deux plans) ;
• on met l'ensemble en rotation autour d'un axe vertical à la vitesse quelconque (fixée par l'expérimentateur).

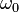
On remarque alors que la surface du liquide se courbe, pour adopter la forme d'une parabole, d'équation identique à celle de la came de Huygens, avec le paramètre valant .