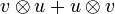Algèbre tensorielle - Définition
La liste des auteurs de cet article est disponible ici.
Généralisation
Pour tout module M sur un anneau commutatif unitaire A, on construit de la même façon une A-algèbre unitaire graduée
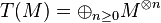
On définit encore l'algèbre symétrique Sym(M) et l'algèbre extérieure ΛM comme dans le cas des espaces vectoriels. L'image de
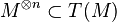
Lorsque M est libre, T(M) (resp. Sym(M)) est isomorphe à l'anneau des polynômes non-commutatif (resp. commutatif) à coefficients dans A à indéterminées indexées par les éléments d'une base.
Pour tout module M de type fini, Sym(M) est une algèbre de type fini sur A. Si M est engendré par d éléments, alors ΛnM = 0 pour tout n > d. Si de plus M est libre de rang d, alors ΛnM est libre pour tout
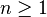
Soit
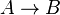
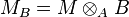
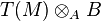
Applications
L'algèbre symétrique sur un espace vectoriel V est le quotient de son algèbre tensorielle par l'idéal engendré par les commutateurs de la forme :
-
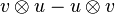
Tout choix d'une base pour V identifie son algèbre symétrique avec l'algèbre des polynômes à indéterminées dans la base.
L'algèbre extérieure sur V est le quotient de son algèbre tensorielle par l'idéal engendré par les anticommutateurs de la forme :
-