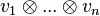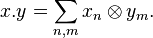Algèbre tensorielle - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
L'algèbre tensorielle au sens de théorie des tenseurs est traitée à l'article « Tenseur ».
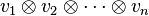
En mathématiques, une algèbre tensorielle est une algèbre sur un corps dont les éléments (appelés tenseurs) sont représentés par des combinaisons linéaires de « mots » formés avec des vecteurs d'un espace vectoriel donné. Les seules relations de dépendance linéaire entre ces mots sont induites par les combinaisons linéaires entre les vecteurs.
Si l'espace vectoriel sous-jacent est muni d'une base, son algèbre tensorielle s'identifie avec l'algèbre associative unitaire libre engendrée par cette base. Si cette base est finie, les tenseurs s'identifient avec des tableaux de coordonnées.
L'algèbre tensorielle permet d'étendre en morphismes d'algèbre toutes les applications linéaires d'un espace vectoriel vers les algèbres associatives unitaires. À ce titre, la construction de l'algèbre tensorielle sur un espace vectoriel est adjointe à gauche à l'oubli de la structure multiplicative.
Divers quotients de l'algèbre tensorielle constituent l'algèbre symétrique, l'algèbre extérieure…
Construction mathématique
Définition par l'algèbre libre
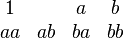
Un mot sur un ensemble est une suite finie d'éléments de cet ensemble, souvent notée sans séparateurs ni parenthèses. L'algèbre libre sur un ensemble E est l'espace vectoriel des familles presque nulles indicées par les mots sur E, muni de la multiplication induite par la concaténation. Chaque mot m est identifié avec la suite qui vaut 1 en m et 0 partout ailleurs.
La non-commutativité des lettres d'un mot empêche certaines simplifications usuelles comme dans l'égalité suivante :
-
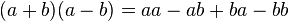
Il n'y a pas d'annulation de (−ab) par (+ba), a contrario de l'identité remarquable valable pour les nombres réels ou complexes.
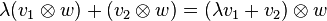
Pour définir l'algèbre tensorielle sur un espace vectoriel V, il suffit de considérer l'algèbre libre engendrée par tous les éléments de V puis de la quotienter par l'idéal engendré par les relations linéaires sur V. L'algèbre quotient est notée T(V). Dans ce cadre, les vecteurs servant de lettres dans chaque mot sont souvent séparées par le symbole du produit tensoriel, semblable à la croix de multiplication inscrite dans un cercle.
Construction par produit tensoriel
On fixe un espace vectoriel V sur un corps K. Pour tout entier
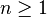
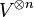
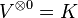
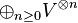
1. Soient
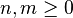
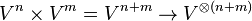
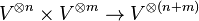
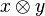
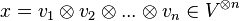
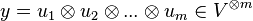
-
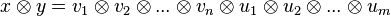
2. On définit alors le produit
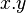
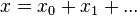
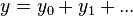
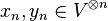
On vérifie que cela définit bien une structure de K-algèbre, et on appelle T(V) l'algèbre tensorielle de V.
Exemples
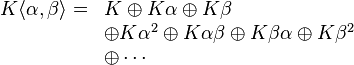
- Si V est un espace vectoriel de dimension 1 engendré par un élément x, l'algèbre tensorielle T(V) s'identifie avec l'algèbre des polynômes à une indéterminée.
- Si V est de dimension quelconque, tout choix d'une base sur V identifie son algèbre tensorielle avec l'algèbre des polynômes non commutatifs à indéterminées dans la base de V. Dans ce cas, les coefficients de ces polynômes constituent les valeurs de tableaux de coordonnées pour représenter chaque tenseur.
Propriétés
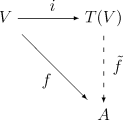
- L'algèbre tensorielle T(V) est une K-algèbre unitaire, non-commutative en général.
- L'algèbre tensorielle est graduée par la longueur des mots. Chaque tenseur se décompose de façon unique en une somme de tenseurs homogènes, c'est-à-dire qui sont combinaisons linéaires de mots de même longueur. Ceci est une traduction de l'écriture de T(V) comme somme directe des
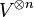
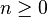
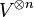
- (Propriété universelle) Pour toute application linéaire f d'un espace vectoriel V vers une algèbre associative unitaire A, il existe un unique morphisme d'algèbre qui étende l'application f à l'algèbre tensorielle T(V). Concrètement, le morphisme envoie