Algorithme de tri - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Un algorithme de tri est, en informatique ou en mathématiques, un algorithme qui permet d'organiser une collection d'objets selon un ordre déterminé. Les objets à trier font donc partie d'un ensemble muni d'une relation d'ordre (de manière générale un ordre total). Les ordres les plus utilisés sont l’ordre numérique et l'ordre lexicographique (dictionnaire).
Suivant la relation d'ordre considérée, une même collection d’objet peut donner lieu à divers arrangements, pourtant il est possible de définir un algorithme de tri indépendamment de la fonction d’ordre utilisée. Celui-ci ne fera qu'utiliser une certaine fonction d’ordre correspondant à une relation d’ordre qui doit permettre de comparer tout couple d'éléments de la collection.
Classification
La classification des algorithmes de tri est très importante, car elle permet de choisir l’algorithme le plus adapté au problème traité, tout en tenant compte des contraintes imposées par celui-ci.
On distingue, tout d'abord, les algorithmes de tri d'application générale, procédant par comparaisons entre des paires d'éléments, et les algorithmes plus spécialisés faisant des hypothèses restrictives sur la structure des données entrées (par exemple, le tri par comptage, applicable uniquement si les données sont prises parmi un petit ensemble connu à l'avance). Si l'on ne précise rien, on entend habituellement par « algorithme de tri » un algorithme général de tri par comparaison.
Les principales caractéristiques qui permettent de différencier les algorithmes de tri sont : la complexité algorithmique, les ressources nécessaires (notamment en termes d'espace mémoire utilisé) et le caractère stable.
Complexité algorithmique
- La complexité algorithmique temporelle dans le pire des cas permet de fixer une borne supérieure du nombre d'opérations qui seront nécessaires pour trier un ensemble de n éléments.
- La complexité algorithmique temporelle en moyenne : c’est le nombre d'opérations élémentaires effectuées en moyenne pour trier une collection d’éléments. Elle permet de comparer les algorithmes de tris et donne une bonne idée du temps d'exécution qui sera nécessaire à l’algorithme ; on arrive à l'estimer avec une précision assez importante. Toutefois, si les ensembles à trier ont une forme particulière et ne sont pas représentatifs des n ! combinaisons possibles, alors les performances pourront être très inférieures ou très supérieures à la complexité « moyenne ».
- La complexité algorithmique spatiale (en moyenne ou dans le pire des cas) représente, quant à elle, l’utilisation mémoire que va nécessiter l'algorithme. Celle-ci peut dépendre, comme le temps d'exécution, du nombre d'éléments à trier.
La complexité, généralement notée T, est exprimée en fonction du nombre n d'éléments à l'aide des notations de Landau : O et Θ. Pour certains des algorithmes de tri les plus simples, T(n) = O(n2), pour les tris plus élaborés, T(n) = O(n·log(n)).
On peut montrer que la complexité temporelle en moyenne et dans le pire des cas d’un algorithme basé sur une fonction de comparaison ne peut pas être meilleure que n·log(n). Les tris qui ne demandent que n·log(n) comparaisons en moyenne sont alors dits optimaux.
Le problème du tri consiste, étant donné une suite u = (u, u, ..., u) d’éléments d’un ensemble totalement ordonné (par exemple

Un algorithme de tri par comparaisons successives se modélise comme un arbre binaire, chaque nœud de l'arbre correspondant à une comparaison entre deux éléments de l'ensemble. On compare deux éléments u et u, et en fonction du résultat, on passe à l'un des deux nœuds suivants, où l'on procède à une autre comparaison. Chaque feuille (nœud terminal) de l'arbre correspond à la suite totalement triée.
L'algorithme doit être en mesure de fournir toutes les possibilités de permutation des termes de la suite, car il est équivalent de fournir la permutation σ et de fournir la suite triée y. Le nombre de permutations de n éléments étant n ! (factorielle n) le nombre de feuilles de l'arbre doit être au moins n ! .
Borne inférieure pour la complexité dans le pire cas
Notons h la profondeur maximale de l'arbre (nous parlons bien d'un nombre d'étapes dans le pire des cas). Le nombre maximal de feuilles dans un arbre binaire de profondeur maximale h est de 2h.
Il vient donc :
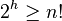
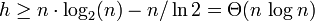
Le fait qu'il existe des tris en
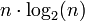
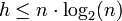
Borne inférieure pour la complexité en moyenne
Étant donné un arbre binaire A, on note F(A) la profondeur moyenne des feuilles de A. Si toutes les permutations des éléments en entrée sont équiprobables, alors le nombre moyen de comparaisons du tri avec un arbre de comparaisons A est égal à F(A).
Pour un nombre de nœuds fixé, les arbres minimisant F sont les arbres binaires complets (c'est-à-dire ceux dont toutes les feuilles sont au dernier ou à l'avant-dernier niveau). En effet, dans un arbre A non complet, il existe une feuille de profondeur h et une feuille de profondeur au plus h-2. En raccrochant la première feuille à la seconde, on obtient un arbre A’ tel que F(A’) < F(A).
La fonction F a la même valeur sur tous les arbres binaires complets à n! feuilles, Soit A l'un d'entre eux, notons h sa hauteur. Toutes les feuilles sont de profondeur au moins h-1, donc la profondeur moyenne des feuilles est au moins
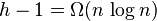
Pour certains types de données (entiers, chaînes de caractères de taille bornée), il existe cependant des algorithmes plus efficaces au niveau du temps d'exécution, comme le tri comptage ou le tri par base. Ces algorithmes n'utilisent pas la comparaison entre éléments (la borne n·log(n) ne s'applique donc pas pour eux) mais nécessitent des hypothèses sur les objets à trier. Par exemple, le tri comptage et le tri par base s'appliquent à des entiers que l'on sait appartenir à l'ensemble [1, m] avec comme hypothèse supplémentaire pour le tri par base que m soit une puissance de 2 (c’est-à-dire de la forme 2k).
Caractère en place
Un algorithme est dit en place s'il n'utilise qu'un nombre très limité de variables et qu’il modifie directement la structure qu’il est en train de trier. Ceci nécessite l’utilisation d'une structure de donnée adaptée (un tableau par exemple). Ce caractère peut être très important si on ne dispose pas d'une grande quantité de mémoire utilisable.
Remarquons toutefois qu'en général, on ne trie pas directement les données elles-mêmes, mais seulement des références (ou pointeurs) sur ces dernières.
Caractère stable
Un algorithme est dit stable s'il garde l'ordre relatif des quantités égales pour la relation d'ordre.
Exemple, si on considère la suite d’éléments suivante :
(4, 1) (3, 1) (3, 7) (5, 6)
que l'on trie par rapport à leur première coordonnée (la clé), deux cas sont possibles, quand l’ordre relatif est respecté et quand il ne l'est pas :
(3, 1) (3, 7) (4, 1) (5, 6) (ordre relatif maintenu) (3, 7) (3, 1) (4, 1) (5, 6) (ordre relatif changé)
Lorsque deux éléments sont égaux pour la relation d'ordre (c’est-à-dire qu'ils ont la même clé), l'algorithme de tri conserve l'ordre dans lequel ces deux éléments se trouvaient avant son exécution. Les algorithmes de tri instables peuvent être retravaillés spécifiquement afin de les rendre stables, cependant cela peut être aux dépens de la rapidité et/ou peut nécessiter un espace mémoire supplémentaire.
Parmi les algorithmes listés plus bas, les tris étant stables sont : le tri à bulles, le tri par insertion et le tri fusion. Les autres algorithmes nécessitent O(n) mémoire supplémentaire pour stocker l'ordre initial des éléments.

















































