Analyse harmonique sur un espace vectoriel fini - Définition
La liste des auteurs de cet article est disponible ici.
Formule sommatoire de Poisson
Si W est un sous-groupe de V et v un élément de l'algèbre du groupe C[V], alors la formule sommatoire de Poisson prend la forme suivante :
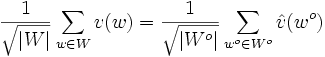
En particulier, si W est autodual, c'est-à-dire si W est confondu avec W°, alors la formule prend la forme suivante :
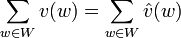
Transformée de Fourier
L'ordre du groupe V est égal à n.q car V est un espace vectoriel de dimension n sur un corps de cardinal q. L'isomorphisme entre V et son dual permet de donner la définition suivante de la transformée de Fourier :
-
- Si u est un élément de C[V] alors sa transformée de Fourier est l'application
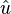
- Si u est un élément de C[V] alors sa transformée de Fourier est l'application

Ce résultat est l'application directe de la définition de la transformée de Fourier et du paragraphe précédent. Ici, le dual de V est identifié à V à l'aide de l'isomorphisme du paragraphe précédent.
Si ( , ) désigne le produit hermitien canonique de l'espace vectoriel complexe C[V] algèbre du groupe V, alors l'égalité suivante dite de Parseval est vérifiée :
![\forall u,v \in \mathbb C[V] \quad (u|v)=(\hat u|\hat v) \;](https://static.techno-science.net/illustration/Definitions/autres/b/bb3b084f7282d665209de1512bc74107_e6366a46a89a085bdb49c948bc61594d.png)
-
- Le théorème de Plancherel prend la forme suivante :
![\forall u \in \mathbb C[V] \quad \forall v \in V \quad u(v)=\frac 1{\sqrt {q^n}}\sum_{\zeta \in V} \hat u (\zeta) \chi_0(<x|\zeta>) \;](https://upload.wikimedia.org/math/9/9/c/99c85b8bc3d4db7b1dd0a0fe5e9d8362.png)
Applications
Fonction booléenne
Il existe un cas particulier, celui où l'espace vectoriel est binaire, c'est-à-dire sur le corps à deux éléments F2. Dans ce contexte, il n'existe qu'un caractère non trivial, celui qui à l'unité associe -1. La transformée de Fourier prend alors une forme simple et porte le nom de transformée de Walsh.
Il possède de nombreuses applications en théorie des codes. Il sert par exemple en cryptographie pour assurer la sécurité d'un message à l'aide d'une boîte-S dans le cas des algorithmes à chiffrement symétrique.
Identité de MacWilliams
L'analyse harmonique sur les espaces vectoriels finis est aussi utilisée pour les codes correcteurs, particulièrement dans le contexte des codes linéaires.
L'identité de MacWilliams est un exemple, elle relie le polynôme énumérateur des poids, c'est-à-dire la distribution des poids de Hamming, d'un code linéaire et celui de son dual. Il sert pour l'étude de code comme celui de Hamming.

















































