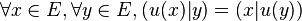Hermitien - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Plusieurs entités mathématiques sont qualifiées d'hermitiennes en référence au mathématicien Charles Hermite.
Produit scalaire hermitien et espace hermitien
Soit E un espace vectoriel complexe. On dit qu'une application f définie sur E x E dans C est une forme sesquilinéaire à gauche si
Quels que soit les vecteurs X, Y, Z , et a, b des scalaires :
- f est semi-linéaire par rapport à la première variable
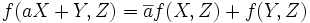
- f est linéaire par rapport à la deuxième variable
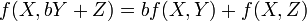
Une telle forme est dite hermitienne (ou à symétrie hermitienne) si de plus
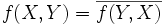
Elle est dite hermitienne définie positive si  pour tout vecteur
pour tout vecteur
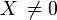
Un produit scalaire hermitien est une forme hermitienne définie positive.
On appelle espace hermitien tout espace vectoriel E complexe de dimension finie muni d'un produit scalaire hermitien.
Les deux exemples de base d'espaces munis de formes hermitiennes sont
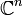
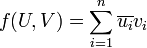
et
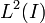
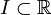
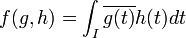
(On considère des fonctions à valeurs complexes : En théorie des séries de Fourier, il est plus commode de travailler avec les exponentielles complexes (e2iπnx) qu'avec les fonctions réelles sinus et cosinus, ce qui explique l'intervention de la notion de forme hermitienne dans la décomposition spectrale de Fourier.)
Les deux propriétés de base d'un produit scalaire réel subsistent :
- l'inégalité de Cauchy-Schwarz ;
-
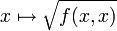
Matrice hermitienne
Une matrice hermitienne (ou auto-adjointe) est une matrice carrée avec des éléments complexes qui vérifie la propriété suivante :
- la matrice est égale à la matrice transconjuguée (matrice transposée de la matrice conjuguée).
En d'autres termes,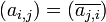
- Exemple
-
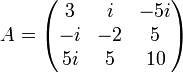
-
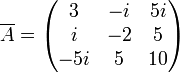
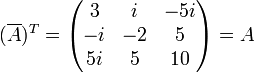
En particulier, une matrice à éléments réels est hermitienne si et seulement si elle est symétrique.
Une matrice hermitienne est orthogonalement diagonalisable et toutes ses valeurs propres sont réelles ; ses sous-espaces propres sont deux à deux orthogonaux.
Opérateur hermitien
Un opérateur u d'un espace hermitien E est dit hermitien si :
Les opérateurs hermitiens jouent un rôle important en mécanique quantique, car ils représentent les grandeurs physiques. Les valeurs propres (réelles) représentent les valeurs possibles de la grandeur et les fonctions propres (ou vecteurs) les états associés.
Dans une base orthonormale, la matrice d'un tel opérateur est égale à la transposée de sa conjuguée, on dit que la matrice est hermitienne (ou auto-adjointe). Notons :
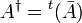
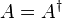
Constantes d'Hermite
L'empilement de n-hypersphères (jusqu'à n=8) le plus dense, en dimension n, donne des structures se rapprochant des n-simplexes (c'est-à-dire triangle, tétraèdre, etc... mais aussi hexagone ou cuboctaèdre). Ces n-simplexes peuvent être entre autres caractérisés par un n-hypervolume ou des nombres: ainsi, les nombres triangulaires sont de la forme a(a + 1) / 2, les nombres tétraédriques: a(a + 1)(a + 2) / 6, etc... la limite du rapport "nombre" sur l'hypervolume, pour "a" tendant vers

D'autres informations sur [1]
Espace euclidien • Espace hermitien • Forme bilinéaire • Forme quadratique • Forme sesquilinéaire • Orthogonalité • Base orthonormale • Projection orthogonale • Inégalité de Cauchy-Schwarz • Inégalité de Minkowski • Matrice positive • Matrice définie positive • Décomposition QR • Déterminant de Gram • Espace de Hilbert • Base de Hilbert • Théorème spectral • Théorème de Stampacchia • Théorème de Riesz • Théorème de Lax-Milgram • Théorème de représentation de Riesz