Arithmétique élémentaire - Définition

Conséquences directes

Théorème de Wilson

Un exemple de résultat d'arithmétique qui peut se démontrer à l'aide des théorèmes énoncés dans cet article est maintenant appelé théorème de Wilson. Il a été démontré par le mathématicien arabe du X^e siècle Alhazen. Il s'énonce ainsi :

Théorème de Wilson — Un entier strictement positif p est un nombre premier si et seulement s'il divise (p - 1)! + 1, c'est-à-dire si, et seulement si :

Une démonstration élémentaire est présentée dans l'article détaillé.

Petit théorème de Fermat

Pierre de Fermat est un mathématicien français du XVII^e siècle que s'est passionné pour l'arithmétique. Le bagage mathématique disponible à son époque était, en arithmétique, plutôt plus faible que celui présenté ici, car l'usage des nombres négatifs était encore problématique. Il a établi le résultat suivant :

L'article détaillé présente une démonstration uniquement à l'aide des outils étudiés dans le cadre de cet article. Par delà l'élégance du résultat, il sert aussi de théorème pour démontrer d'autres résultats d'arithmétiques. Il est utilisé, par exemple pour une démonstration élémentaire du théorème des deux carrés de Fermat. Ce résultat stipule que si p est un nombre premier ayant pour reste 1 s'il est divisé par 4, alors l'équation X² + Y² = p admet toujours une solution.

Test de Primalité

Le petit théorème de Fermat est à la base de nombreux tests de primalité. Pour en comprendre le principe appliquons sa forme naïve au cinquième nombre de Fermat, noté F₅ et égal à 2³² + 1, ou encore à 4 294 967 297. Fermat a toujours cru que ce nombre était premier, il écrit « ... je n'ai pu encore démontrer nécessairement la vérité de cette proposition ». C'est la seule conjecture fausse que Fermat a émise.

La méthode simple et brutale, consiste à calculer le reste de la division de a^(F₅ - 1) - 1 par F₅. Si le reste n'est nul, le nombre n'est pas premier. Avec deux astuces, les calculs sont beaucoup plus simples qu'il n'y paraît, choisissons a égal à 3. Son carré donne a², égal à 9. le carré de ce nombre donne 3²², égal à 81, son carré est égal à 3²³ 6 561. Comme F₅ - 1 est égal à 2³², il suffit de 32 étapes pour conclure, ce qui est maintenant rapide avec les méthodes de calculs modernes.

La deuxième difficulté à résoudre est le caractère élevé des puissances successives, on finirait par devoir utiliser des très grands nombres qui imposent une écriture lourde des valeurs intermédiaires, ainsi 3²⁵ est égal à 1 853 020 188 851 841, alors que ce n'est que la cinquième valeur intermédiaire et qu'il faut en calculer 32. Il est néanmoins possible d'écrire ce nombre habilement, à l'aide d'une division euclidienne :

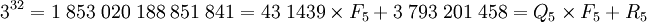
Ce qui importe, c'est le reste de la division euclidienne de 3^(F₅ - 1) - 1 et non pas la valeur de Q₅. Ainsi, à l'étape d'après :

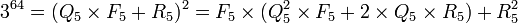
Il suffit que calculer le carré de R₅ et d'opérer une division euclidienne de ce carré par F₅ et on obtient :

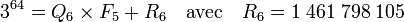
Le calcul de Q₆, et en règle générale de Q_n où n est un entier qui va jusqu'à 32, est inutile. Et la suite des R_n ne dépasse jamais F₅, ce qui empêche une explosion de chiffres significatifs à calculer. En 32 étapes, on trouve que le reste de la division euclidienne de 3^(F₅ - 1) - 1 par F₅ est égal à 3 029 026 159 et non pas 0, le nombre F₅ n'est pas premier. Euler utilise une méthode plus habile, elle exhibe effectivement les diviseurs, sa méthode est exposée dans l'article Nombre de Fermat.