Arithmétique élémentaire - Définition

Introduction

L’arithmétique élémentaire regroupe les rudiments de la connaissance des nombres telle qu'elle est présentée dans l'enseignement des mathématiques. Elle commence avec la comptine numérique, autrement dit la suite des premiers entiers à partir de 1, apprise comme une liste ou une récitation et utilisée pour dénombrer de petites quantités. Viennent ensuite les opérations d'addition et de multiplication par le biais des table d'addition et table de multiplication. Ces opérations permettent, dans le cadre de l'algèbre, de définir leurs opérations réciproques : la soustraction et la division. Ce savoir n'est pas couvert par cet article.

L'apprentissage des tables de multiplication conduit ensuite à la reconnaissance des critères de divisibilité par 2, par 3, par 5, par 9 et par 10, puis à la décomposition des entiers en facteurs premiers. L'unicité de cette décomposition permet la définition du plus grand commun diviseur (pgcd) et du plus petit commun multiple (ppcm). La division euclidienne est utilisée dans l'algorithme d'Euclide pour calculer le pgcd de deux nombres sans connaître leur décomposition en facteurs premiers.

Un premier niveau de savoir se dégage, avec quelques lemmes et théorèmes clés, comme le lemme d'Euclide, l'identité de Bézout et le théorème fondamental de l'arithmétique. Il suffit à démontrer quelques résultats comme le petit théorème de Fermat, celui de Wilson et quelques équations peuvent être résolues. Les équations en questions sont dites diophantiennes, c'est-à-dire qu'elles sont à coefficients entiers et les solutions recherchées sont entières. La méthode chakravala permet de trouver une solution à l'équation X² - 83Y² = 1 dès le VI^e siècle. Ces méthodes permettent encore à Euler, un mathématicien suisse du XVIII^e siècle, de résoudre l'équation X² + Y² = p, qui correspond au théorème des deux carrés de Fermat, ici p désigne un nombre premier. Ce sont ces méthodes, couramment considérés comme de l'arithmétique élémentaire, qui sont exposées dans cet article.

Comprendre plus profondément l'arithmétique des nombres entiers impose l'usage de structures abstraites, comme celles des groupes finis, par exemple dans le cadre de l'arithmétique modulaire, ou des anneaux. On quitte alors l'arithmétique élémentaire pour entrer dans la théorie algébrique des nombres.

Division euclidienne

Théorème de la division

L'ensemble étudié dans cet article, noté Z, est celui des nombres entiers, qu'ils soient positifs ou négatifs. L'existence de nombres négatifs offre un avantage trop puissant pour que l'on puisse aisément s'en passer. Initialement, il introduit une petite complexité, comment définir la division euclidienne sur Z ? Il est nécessaire de modifier un peu le résultat déjà connu pour les entiers positifs.

Par rapport à la division euclidienne dans les nombres entiers positifs, une propriété a été perdue, l'unicité de la solution n'est maintenant plus toujours vraie. Considérons l'entier 10 que l'on souhaite diviser par 3, il peut s'écrire de deux manières : 3x3 + 1 ou encore 3x4 + (-2). Autoriser les nombres négatifs, en particulier pour le reste, impose d'admettre deux solutions au lieu d'une, ce qui s'avère n'être que peu gênant. La démonstration de ce résultat est proposée dans l'article détaillé.

Sous-ensembles stables

L'objectif de ce paragraphe est la recherche des sous-ensembles de Z qui sont à la fois non vides et stables pour l'addition et la soustraction. Cette démarche, consistant à étudier la structure de l'ensemble Z, est une des idées fondatrices de l'arithmétique au sens moderne du terme. Dans un contexte plus sophistiqué, ces sous-ensembles peuvent être vus comme des sous-groupes ou des idéaux. L'usage de ces concepts s'avère néanmoins inutile pour une étude qui se limite à l'arithmétique élémentaire.

La démonstration comporte trois parties.

• Tout ensemble de multiple est non vide et stable au sens de la proposition :

Une première partie de la démonstration est aisée à démontrer. Un ensemble de multiples de m est non vide car il contient m. Il est stable par addition et multiplication car si a.m et b.m sont deux multiples de m (ici a et b désignent des nombres entiers) alors a.m +b.m est égal à (a + b).m et a.m -b.m est égal à (a - b).m, la somme et la différence de deux multiples de m sont encore des multiples.

La réciproque fait appel à la division euclidienne. On suppose maintenant que M est un sous-ensemble non vide et stable. Un premier cas se dessine si M est l'ensemble {0}, il est bien stable au sens de la proposition ci-dessus et correspond bien à un ensemble de multiples, celui de l'entier 0. Si M n'est pas réduit à l'ensemble {0}, il contient un élément a ainsi que son inverse -a. Autrement dit il contient un élément strictement positif. Soit m le plus petit élément strictement positif de M. On souhaite montrer que tout élément b de M est un multiple de m et que tout multiple de m est élément de M.

• Tout multiple de m est élément de M :

On remarque d'abord que 0 = 0.m est élément de M, en effet, m - m est élément de M car M est stable par soustraction. Soit a.m un multiple de m, si a est strictement positif, a.m peut être vu comme la somme de m : m + m + ... + m répétée a fois, la stabilité de l'addition montre que a.m est bien élément de m. Si a est strictement négatif, -a.m est élément de M et la stabilité de la soustraction montre que 0 - (-a.m) égal à a.m est encore élément de M, ce qui termine cette démonstration.

• Tout élément de M est un multiple de m :

C'est ici qu'intervient la division euclidienne. Soit b un élément de M, considérons la division euclidienne de b par m :

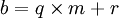
A la fois r et -r sont éléments de M et l'un des deux entiers est positif. Il est non seulement positif mais aussi strictement plus petit que m, ce qui ,par définition de m, montre que r est égal à 0. autrement dit, b est bien un multiple de m car égal à q.m.

Les deux dernières propositions montrent bien que M est l'ensemble des multiples de m, ce qui permet de conclure.