Arithmétique élémentaire - Définition

Théorème fondamental de l'arithmétique

Théorème de Bachet-Bézout

Une identité permet de venir à bout de toute équation diophantienne du premier degré. Une forme faible de l'identité est la suivante :

Identité de Bachet-Bézout — Deux nombres entiers a et b sont premiers entre eux si, et seulement si, il existe deux entier m et n tel que :

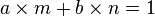
Cette forme de l'identité de Bachet-Bézout est plus faible que celle de l'article détaillé et cela à deux titres. Tout d'abord, elle ne traite que du cas où a et b sont premiers entre eux, ensuite l'article détaillé donne une méthode effective pour trouver les valeurs de m et n, ce qui n'est pas le propos de ce paragraphe.

Pour démontrer cette identité, on peut remarquer que l'ensemble M des nombres de la forme a.m + b.n, si m et n décrivent tous les entiers, est non vide et stable pour l'addition et la multiplication. La proposition précédente montre l'existence d'un entier m tel que M soit l'ensemble des multiples de m. Si a et b sont premiers entre eux, l'entier m, qui divise a et b, car ce sont des éléments de M, est nécessairement égal à 1 ou -1. Les multiples de m forment l'ensemble Z tout entier, qui contient 1, ce qui montre l'existence d'une solution à l'identité.

Si a et b comporte un diviseur commun c, différent de 1 et de -1, l'expression a.m + b.n est aussi un multiple de c et ne peut être égale à 1, qui lui ne l'est pas.

Lemme d'Euclide

Une application importante de l'identité du dernier paragraphe est le lemme d'Euclide :

Ce lemme fait apparaitre des nombres essentiels en arithmétique, les nombres premiers. Ce sont des nombres strictement positifs qui n'ont comme diviseurs positifs qu'eux-mêmes et un. Le mathématicien Paul Erdös disaient d'eux : « Un nombre premier est un nombre qui ne se casse pas quand on le laisse tomber par terre. ». Ce lemme est une étape pour démontrer le théorème fondamental de l'arithmétique.

Sa démonstration fait appel à l'identité précédente et est démontrée dans l'article détaillé.

Théorème fondamental de l'arithmétique

Si l'on considère un entier quelconque, on peut l'écrire sous la forme ε.a, où ε désigne soit 1 où -1 et a un nombre entier positif. Si a n'est pas premier, il se décompose en un produit c.b de nombres entiers positifs, opération que l'on peut recommencer. On finit par trouver une décomposition en facteurs premiers :

Ce théorème est le résultat clé de l'arithmétique élémentaire, démontré dans l'article détaillé. Sous une forme plus ou moins générale, il est à la base de nombreux résultats qui se démontrent à l'aide de l'arithmétique élémentaire. En conséquence, la connaissance des nombres premiers s'avère essentielle. Cette connaissance est parfois difficile, leur répartition, par exemple, est en 2008, encore l'objet d'une des plus célèbres conjecture des mathématiques (voir l'article hypothèse de Riemann qui dépasse de loin le cadre de l'arithmétique élémentaire). On dispose néanmoins aisément d'un premier résultat :

Pour s'en rendre compte, il suffit de considérer un ensemble fini F de nombres premiers et de montrer que cet ensemble ne les contient pas tous. Soit m la somme de 1 et du produit de tous les nombres de F. L'entier m n'est divisible par aucun élément de F, soit il est premier, soit il est divisible par un nombre premier qui n'est pas dans la liste. En conséquence F ne contient pas tous les nombres premiers. Dire qu'aucun ensemble fini contient tous les nombres premiers, c'est dire que le nombre de nombres premiers est infini (cf Théorème d'Euclide sur les nombres premiers).