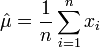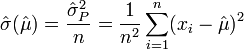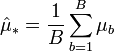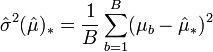Bootstrap (statistiques) - Définition
La liste des auteurs de cet article est disponible ici.
Exemple
On utilise 34 des 507 observations concernant les dimensions du corps humains. On extrait le poids (en kilo) et la taille (en mètre), afin de calculer l'Indice de masse corporelle, défini comme le ratio du poids et de la taille au carré. Les données sont reproduites ci-dessous.
| poids | taille | IMC |
|---|---|---|
| 65,60 | 1,74 | 21,67 |
| 71,80 | 1,75 | 23,36 |
| 80,70 | 1,94 | 21,55 |
| 72,60 | 1,87 | 20,87 |
| 78,80 | 1,87 | 22,49 |
| 74,80 | 1,82 | 22,71 |
| 62,00 | 1,75 | 20,24 |
| 81,60 | 1,84 | 24,10 |
| 76,60 | 1,80 | 23,64 |
| 83,60 | 1,78 | 26,44 |
| 74,60 | 1,76 | 24,08 |
| 76,40 | 1,80 | 23,50 |
| 63,20 | 1,65 | 23,36 |
| 60,90 | 1,73 | 20,35 |
| 74,80 | 1,84 | 22,21 |
| 59,50 | 1,70 | 20,59 |
| 67,20 | 1,82 | 20,29 |
| 61,30 | 1,70 | 21,21 |
| 68,60 | 1,78 | 21,70 |
| 55,20 | 1,64 | 20,50 |
| 57,00 | 1,63 | 21,45 |
| 66,10 | 1,72 | 22,40 |
| 72,00 | 1,82 | 21,74 |
| 64,60 | 1,67 | 23,16 |
| 74,80 | 1,78 | 23,66 |
| 70,00 | 1,65 | 25,87 |
| 68,40 | 1,77 | 21,96 |
| 65,90 | 1,69 | 22,96 |
| 75,70 | 1,82 | 22,83 |
| 73,20 | 1,77 | 23,29 |
| 53,90 | 1,67 | 19,23 |
| 72,00 | 1,78 | 22,70 |
| 55,50 | 1,69 | 19,46 |
| 58,40 | 1,57 | 23,63 |
On s'intéresse à l'espérance μ de l'IMC, et surtout à sa variance. L'estimateur naturel est la moyenne empirique:
et l'estimateur de sa variance, noté , est connu explicitement : c'est l'estimateur de la variance de la population, divisé par n, c'est-à-dire :
Les estimations empiriques sont
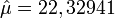
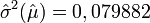
On peut comparer aux résultats obtenus grâce aux techniques bootstrap. On utilise B = 1000 échantillons bootstrap, de dimension n = 34. On rappelle la procédure à suivre :
- pour b allant de 1 à B
- on construit un échantillon bootstrap par rééchantillonnage avec remise ;
- on calcule la moyenne empirique à partir de l'échantillon bootstrap précédent, noté μb ;
- on calcule la moyenne et la variance de la distribution bootstrap.
Ces calculs sont les suivants :
et
La distribution bootstrap (c'est-à-dire la distribution des moyennes empiriques obtenues à partir des 1000 échantillons bootstrap) est représentée dans la figure ci-contre. La moyenne empirique est
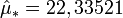
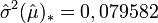
Bibliothèque logicielle
- librairie gratuite pour Matlab
- Sous R, il existe principalement deux paquets :
- bootstrap basé sur Efron et Tibshirani (1994) ;
- boot présente plus de fonctionnalités (d’après Davison et Hinkley, 1997).