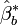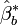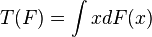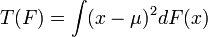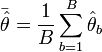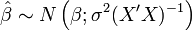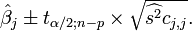Bootstrap (statistiques) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En Statistiques, les techniques de bootstrap sont des méthodes d'Inférence statistique modernes, datant de la fin des années 70, et requérant des calculs informatiques intensifs. L'objectif est de connaître certaines indications sur une statistique : son estimation bien sûr, mais aussi la dispersion (variance, écart-type), des intervalles de confiance voire un Test d'hypothèse. Cette méthode est basée sur des simulations, comme les méthodes de Monte-Carlo, les méthodes numériques bayésiennes (échantillonneur de Gibbs (en), l'algorithme de Metropolis-Hastings (en)), à la différence près que le bootstrap ne nécessite pas d'information supplémentaire que celle disponible dans l'échantillon. En général, il est basé sur de « nouveaux échantillons » obtenus par tirage avec remise à partir de l'échantillon initial (on parle de rééchantillonnage).
L'aspect autocentré et itératif de la méthode a inspiré sa désignation anglaise : en effet, le bootstrap désigne le fait de « se hisser en tirant sur ses propres lacets ou plus précisément sur ses « bootstraps » qui désignent en anglais les anneaux de cuir ou tissu cousus au rebord des bottes pour y passer les doigts afin de les enfiler plus facilement ».
Principe général
Soit un échantillon
et dans le dernier
avec μ l'espérance, dont l'expression a été donnée plus haut.
Une estimation classique de θ est
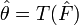
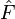
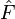
- cas paramétrique : on suppose que F fait partie d'une famille de lois paramétriques, c'est-à-dire indexées par un ensemble de paramètres, disons ω. Après l'estimation des paramètres ω, par maximum de vraisemblance par exemple, on dispose d'une estimation (paramétrique) de F. On parle de bootstrap paramétrique ;
- cas non paramétrique : ici, on ne fait aucune hypothèse sur l'appartenance de la loi à une famille paramétrique. On estime
L'étape suivante du bootstrap se base sur des simulations : étant donné l'estimation (paramétrique ou non)
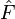
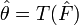
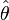
Pour le cas paramétrique, la méthode de bootstrap s'apparente aux méthodes simulées comme les méthodes de Monte-Carlo. Dans le cas non-paramétrique, la méthode du bootstrap revient à utiliser un échantillon bootstrap composé d'un rééchantillonnage avec remise de l'échantillon initial. La méthode nécessite donc des échantillons simulés ; leur nombre, disons B, doit être assez grand pour assurer la convergence des estimations empiriques de
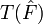
Pour plus de clarté, supposons que l'on veuille estimer l'espérance de la loi, et surtout sa précision (c´est-à-dire sa variance). Voici comment procéder. On fixe d'abord le nombre B d'échantillons. La procédure se déroule comme suit :
- Boucle : pour b allant de 1 à B:
- on tire un échantillon bootstrap :
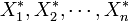
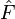
- on calcule la statistique (ici la moyenne empirique) à partir de l'échantillon bootstrap :
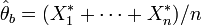
- on tire un échantillon bootstrap :
- La variance de l'estimateur de l'espérance est approchée par la variance empirique de la population bootstrap des
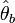
Dans cette dernière étape, on a à estimer
-
![v^2_b = \frac{1}{B} \sum_{b=1}^B \left[\hat\theta_b -\bar\hat\theta\right]^2](https://static.techno-science.net/illustration/Definitions/autres/b/b54e09d14e2d1959699457599404ca0d_cf727663a6b2eff45affcedf4a3b2b60.png)
avec
qui constitue une alternative à l'estimateur classique
-
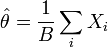
Pour le bootstrap non-paramétrique, l'étape de simulation est très simple : il s'agit d'un échantillon bootstrap obtenu tout simplement par rééchantillonnage avec remise de l'échantillon initial. Par exemple, pour un échantillon initial (1,2,5,4), un échantillon bootstrap sera par exemple (5,5,4,1) ou encore (4,1,4,2) et ainsi de suite.
Intervalle de confiance
Le bootstrap permet aussi de donner une idée de l'intervalle de confiance d'une estimation. Un intervalle de confiance bootstrap, au niveau α, se détermine en identifiant les Quantiles de la distribution bootstrap, en laissant de part et d'autre de la distribution
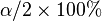
Pour obtenir un intervalle de confiance bootstrap, un nombre de simulations B nécessite d'être suffisamment grand ; en particulier
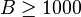
Cette technique n'est valable que lorsque la distribution bootstrap est symétrique et centrée sur l'échantillon original. On consultera avec profit les ouvrages cités en bibliographie pour déterminer les techniques — plus ou moins triviales — permettant d'appréhender ce cas.
Régression linéaire
Le bootstrap peut aussi s'appliquer à la détermination de l'intervalle de confiance pour le paramètre β dans le cas de la régression linéaire classique. Ce cas est dénommé smooth boostrap en anglais.
Dans le modèle de régression linéaire
- y = Xβ + ε,
on suppose que la variable dépendante y et les aléas ε sont de dimension n × 1, les explicatives X de dimension n × p et qu'il y a p coefficients β à déterminer.
Les hypothèses classiques de la régression linéaire permettent de conclure que l'estimateur de β par les moindres carrés ordinaires,
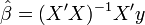
Ainsi, pour un j entre 1 et p, on peut construire un intervalle de confiance au seuil de α % pour
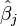
Dans cette formule, tα / 2;n − p est le quantile issu de la loi de Student,
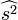
Le bootstrap s'utilise pour fournir une alternative à cet intervalle de confiance. Les aléas ε ne sont pas observables, car leur loi est inconnue. Dans la démarche bootstrap,les aléas sont remplacés par les résidus :
Le bootstrap se déroule comme suit :
- Pour b allant de 1 à B :
- rééchantillonnage : on remplace les aléas par des résidus bootstrap
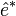
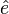
- on construit des variables dépendantes bootstrap :
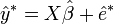
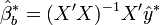
- rééchantillonnage : on remplace les aléas par des résidus bootstrap
- Exploitation de la population des