Calcul du volume de l'hypersphère - Définition

Généralisations ultérieures

Cette méthode d'intégration peut être généralisée aux espaces L^p où En effet, nous avons une relation de récurrence pour les boules unitaires

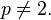
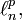
de laquelle on peut retrouver la formule

pour le volume de la boule de rayon r en la mesure de volume étant, comme auparavant, celle de Lebesgue en coordonnées orthonormales. Il n'est plus possible de calculer l'aire de la surface comme la dérivée du volume par rapport au rayon parce que le rayon n'est plus partout normal à la surface.

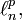
Cette généralisation est d'un intérêt pour la théorie de l'information et la théorie du codage de l'information.