Claude Shannon - Définition

Anecdotes

• En 1981, Claude Shannon a commencé à écrire un article intitulé Scientific Aspects of Juggling, sur l'art de la jonglerie. Cet article était prévu pour être publié dans Scientific American, mais ce ne fut finalement pas le cas. Néanmoins, cette ébauche a servi de base à la formalisation des mouvements de jonglerie par le siteswap.

Son œuvre

Pendant la Seconde Guerre mondiale, Shannon travaille pour les services secrets de l'armée, en cryptographie, chargé de localiser de manière automatique dans le code ennemi les parties signifiantes cachées au milieu du brouillage. Son travail est exposé dans un rapport secret (déclassifié dans les années 1980 seulement), qui donne naissance après-guerre à un article, A Mathematical Theory of Communications (1948), qui fut repris en 1949 sous forme de livre avec un ajout de Warren Weaver, son supérieur dans les services secrets. Cet ouvrage est centré autour de la problématique de la transmission du signal.

Le schéma de Shannon

Pour décrire la communication entre machines, l'article de 1948 et le livre de 1949 commencent tous deux par un « schéma » qui connut dès lors une postérité étonnante en Sciences de l'information et de la communication, au point que Shannon s'en étonna et s'en dissocia. Le schéma modélise la communication entre machines :

Ce schéma est la traduction « civile » d'un schéma préalable, utilisé dans le contexte militaire :

• source → encodeur → signal → décodeur → destinataire, dans un contexte de brouillage.

Adéquat à décrire la communication entre machines, ce schéma modélise imparfaitement la communication humaine. Pourtant, son succès est foudroyant, et il a participé largement à la création d'un champ disciplinaire, les sciences de l'information et de la communication. L'une des explications de ce succès est le fait qu'il se fond parfaitement dans une approche béhavioriste des médias. De plus, ce schéma dit canonique donne une consistance et une apparence de scientificité.

Shannon : l'unité de mesure

Dans l'article comme dans le livre, il popularise l'utilisation du mot bit comme mesure élémentaire de l'information numérique. John Tukey fut néanmoins le premier à utiliser le terme. Plus précisement, le bit désigne le nombre de chiffres binaires nécessaires pour coder une quantité d'information. Ainsi, il faut au moins un bit (ou 1 Shannon) pour coder deux états (par exemple « pile » et « face », ou plus généralement 0 et 1) et deux bits permettent de coder quatre états (00, 01, 10, 11). Les 26 lettres de l'alphabet nécessitent au minimum 5 bits car:

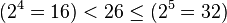
Plus généralement, si P est le nombre d'états possibles, le nombre de bits n nécessaire à tous les coder vérifie:

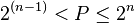
Dans un cas idéal où toute l'information disponible est utilisée, P = 2ⁿ.

La relation de Shannon

Dans le domaine des télécommunications, la relation de Shannon permet de calculer la valence (ou nombre maximal d'états) en milieu perturbé :

Soit S le signal, N le bruit :

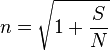
On a alors le débit maximal :

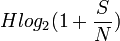
Ce résultat est indépendant de la vitesse d'échantillonnage et du nombre de niveau d'un échantillon (la valence).

Entropie au sens de Shannon

Un apport essentiel des travaux de Shannon concerne la notion d'entropie. Si l'on considère N événements de probabilité p₁, p₂… p_N, indépendants les uns des autres, alors leur entropie de Shannon est définie comme :

Entropie =

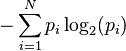
Il a par ailleurs :

• établi un rapport entre augmentation d'entropie et gain d'information ;
• montré l'équivalence de cette notion avec l’ entropie de Ludwig Boltzmann en thermodynamique.

La découverte du concept ouvrait ainsi la voie aux méthodes dites d'entropie maximale (voir probabilité), donc au scanner médical, à la reconnaissance automatique des caractères et à l'apprentissage automatique.

Théorèmes

Son nom est associé à plusieurs théorèmes, le Théorème d'échantillonnage de Nyquist-Shannon sur l'échantillonnage, le premier théorème de Shannon sur la limite théorique de la compression, le deuxième théorème de Shannon sur la capacité d'un canal de transmission.