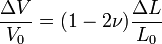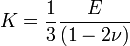Coefficient de Poisson - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Mis en évidence (analytiquement) par Siméon Denis Poisson, le coefficient de Poisson (aussi appelé coefficient principal de Poisson) permet de caractériser la contraction de la matière perpendiculairement à la direction de l'effort appliqué.
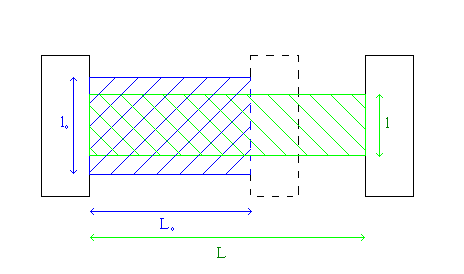
Définition
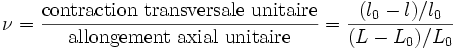
Le coefficient de Poisson fait partie des constantes élastiques. Il est compris entre -1 et 0,5. Les valeurs expérimentales obtenues dans le cas d'un matériau parfaitement isotrope sont très proches de la valeur théorique (1/4). Pour un matériau quelconque, on obtient en moyenne 0,3. Il existe également des matériaux à coefficient de Poisson négatif : on parle alors parfois de matériaux auxétiques.
Quelques valeurs numériques de coefficients de Poisson
Les caractéristiques mécaniques des matériaux sont variables d'un échantillon à l'autre. Néanmoins, pour les calculs, on peut considérer en bonne approximation les valeurs suivantes. Le coefficient de Poisson n'a pas d'unité!
|
|
|
Relations
Cas d'un matériau isotrope
- Le changement de volume ΔV/V dû à la contraction du matériau peut être donné par la formule (uniquement valable pour de petites déformations):
Soit un cube constitué d'un matériau isotrope d'un volume initial
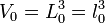
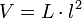
La loi de Poisson s'écrit alors:
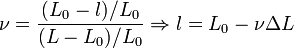
D'où le volume final du cube:
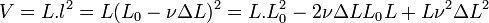
en divisant cette relation par le volume initial
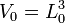
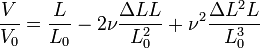
On fait maintenant apparaitre l'expression
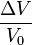
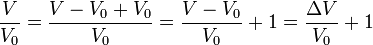
D'où:
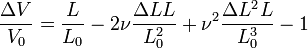
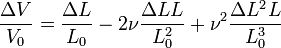
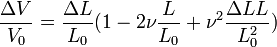
L'hypothèse de petites déformations permet de négliger les termes du second ordre. En approximant
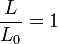
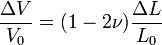
- Le module d'élasticité isostatique (K) est lié au Module de Young (E) par le coefficient de Poisson au travers de la relation :
Cette relation montre que ν doit rester inférieur à 1/2 pour que le module d'élasticité isostatique reste positif (sinon le matériau gonflerait dès qu'on essayerait de le comprimer). On note également les valeurs particulières de ν :
-
- pour ν = 0,33 on a K = E.
- pour ν → 0,5 on a K → ∞ incompressibilité (cas du caoutchouc, par exemple)
- Avec le module de Young (E) exprimé en fonction du module de cisaillement (G) et de ν :
-
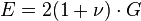
Cette relation met en évidence le fait que ν ne peut être inférieur à -1, sinon son module de cisaillement serait négatif (il serait sollicité en traction dès qu'on le comprimerait!)
Cas d'un stratifié (isotrope transverse)
Un coefficient secondaire de Poisson est alors défini par la relation suivante :
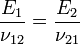
Où E1 et E2 sont les modules de Young des matériaux et ν21 est le coefficient secondaire de Poisson.