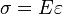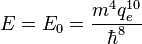Module de Young - Définition

Introduction

Le module de Young ou module d'élasticité (longitudinale) ou encore module de traction est la constante qui relie la contrainte de traction (ou de compression) et la déformation pour un matériau élastique isotrope.

Le physicien britannique Thomas Young (1773-1829) avait remarqué que le rapport entre la contrainte de traction appliquée à un matériau et la déformation qui en résulte (un allongement relatif) est constant, tant que cette déformation reste petite et que la limite d'élasticité du matériau n'est pas atteinte. La loi d'élasticité est la loi de Hooke :

Diagramme contrainte-déformation

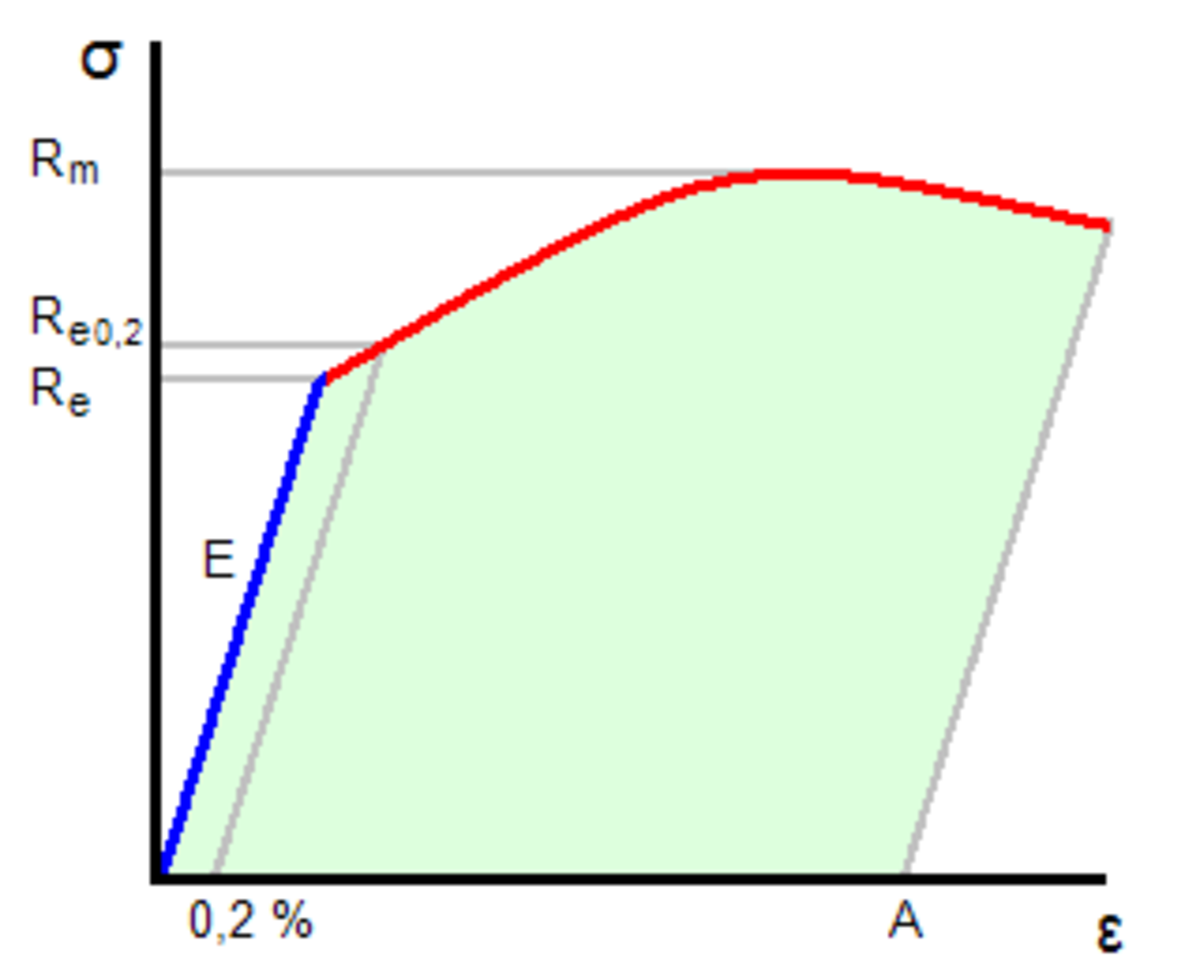
où :

• σ est la contrainte (en unité de pression),
• E est le module de Young (en unité de pression),
• est l'allongement relatif (adimensionnel).

Le module de Young est la contrainte mécanique qui engendrerait un allongement de 100 % de la longueur initiale d'un matériau (il doublerait donc de longueur), si l'on pouvait l'appliquer réellement : dans les faits, le matériau se déforme de façon permanente, ou se rompt, bien avant que cette valeur soit atteinte.

Un matériau dont le module de Young est très élevé est dit rigide. L'acier, l'iridium, le diamant, sont des matériaux très rigides, l'aluminium et le plomb le sont moins, les matières plastiques et organiques sont généralement peu rigides. Il ne faut cependant pas confondre élasticité et rigidité puisque la raideur d'une poutre par exemple dépend de son module de Young mais aussi du moment d'inertie de sa section.

Note
Il ne faut pas confondre rigidité et raideur. La rigidité caractérise les matériaux, la raideur concerne les produits et les constructions. Une pièce mécanique massive en matière plastique peut être beaucoup plus raide qu'un ressort en acier.

Unités

D'après l'équation aux dimensions, le module de Young est homogène à une pression, ou plus précisément une contrainte. L'unité internationale est donc le pascal (Pa). Cependant, en raison des valeurs élevées que prend ce module, il est en général donné en mégapascal (MPa) ou newton par millimètre carré (N/mm²).

Relations

Avec le module de cisaillement (G) et le coefficient de Poisson (ν) :

.

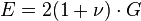
Avec λ et μ appelées coefficients de Lamé :

.

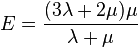
Expression théorique

Dans le cas d'un matériau cristallin et certains matériaux amorphes, le module de Young exprime la « force de rappel » électrostatique qui tend à maintenir les atomes à distance constante. Il peut s'exprimer en fonction de la dérivée seconde du potentiel interatomique.

Dans le système d'unités « naturelles » atomique, le module de Young, pour un matériau isotrope, est homogène à :

où .

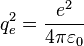
Cela dit, compte tenu des problèmes où il apparaît (bilaplacien), il paraît assez naturel de le rationaliser soit

• comme E₁ = E₀ / (16π²), soit
• comme E₂ = E₀ / 64π⁶,

les ordres de grandeur de E₁ ou E₂ sont à comparer aux valeurs tabulées, de l'ordre de 100 GPa, qui apparaissent alors relever de ce corpus théorique.

Dans le cas des polymères, c'est l'agitation thermique qui « tortille » la chaîne carbonée qui tend à maintenir la longueur de la chaîne constante. Le module de Young peut alors s'exprimer en fonction de l'entropie.

Cette différence de comportement est flagrante lorsque l'on considère l'influence de la température ; si l'on soumet une éprouvette à une charge constante :

• lorsque l'on augmente la température, une éprouvette de métal s'allonge (dilatation), donc son module de Young diminue, tandis que l'éprouvette en polymère se raccourcit (les chaînes s'agitent, s'entortillent) donc son module de Young augmente ;
• lorsque l'on diminue la température, on observe le phénomène inverse : l'éprouvette de métal se raccourcit (contraction) donc son module de Young augmente, tandis que l'éprouvette de polymère s'allonge (les chaînes sont moins agitées et se laissent étirer) donc son module de Young diminue.