Congruence sur les entiers - Définition
La liste des auteurs de cet article est disponible ici.
Congruence modulo n
Définition
Deux entiers a et b sont dits congruents modulo n, où n est un entier supérieur ou égal à 2, si l'une des conditions équivalentes suivantes est vérifiée :
- leur différence est divisible par n ; (il existe un entier k tel que a − b = kn )
- le reste de la division euclidienne de a par n est égal à celui de la division de b par n ;
-
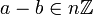
Notation
Si a et b sont congruents modulo n, on écrira :
- a ≡ b (n) ou a ≡ b [n] ou encore a ≡ b (mod n)
ce qui se lit dans tous les cas « a est congru à b modulo n ».
Par exemple :
- 26 ≡ 12 (14)
Le caractère utilisé est ≡. Cependant, par commodité, il est parfois remplacé par = même si cela reste faux dans l'absolu .
Propriétés
Relation d'équivalence
La congruence modulo n a les propriétés suivantes :
- Réflexivité :
- Pour tout entier a, a ≡ a (n)
- Symétrie :
- Pour tous entiers a et b, a ≡ b (n) ⇔ b ≡ a (n)
- Transitivité :
- Pour tous entiers a, b et c, si a ≡ b (n) et b ≡ c (n) alors a ≡ c (n)
Il s'agit donc d'une relation d'équivalence.
Propriétés algébriques
Elle a de plus des propriétés algébriques remarquables :
Si
- a1 ≡ b1 (n) et a2 ≡ b2 (n)
alors
- a1 + a2 ≡ b1 + b2 (n),
- a1a2 ≡ b1b2 (n), et
- a1q ≡ b1q (n), pour n'importe quel entier naturel q supérieur ou égal à 1.
Par hypothèse, a1 = x1 n + b1 et a2 = x2 n + b2.
- Pour l'addition : a1 + a2 = (x1 + x2) n + (b1 + b2 ) ≡ b1 + b2 (n).
- Multiplication :
- a1 a2 = x1 x2 n 2 + (x1 b2 + b1 x2) n + b1 b2 = (x1 x2 n + x1 b2 + b1 x2) n + b1 b2 ≡ b1b2 (n).
- Élévation à n'importe quelle puissance : on applique de façon répétée la propriété ci-dessus de la multiplication,
- pour a2=a1 et b2=b1, puis
- pour a2=a12 et b2=b12,
- pour a2=a13 et b2=b13, etc.
- on obtient ainsi de proche en proche :
- a12 ≡ b12 (n), puis
- a13 ≡ b13 (n),
- a14 ≡ b14 (n), etc.
- (Cette démonstration peut être formalisée par un raisonnement par récurrence.)
On peut parler d'une certaine « compatibilité » avec les opérations d'addition et de multiplication des entiers, c'est-à-dire de « compatibilité » avec la structure d'anneau de (Z,+,*)). Ces quelques propriétés vont nous permettre de définir le domaine de l'arithmétique modulaire : les ensembles quotients Z/nZ.

















































