Conjecture de Syracuse - Définition

Première approche et vocabulaire

La suite de Syracuse d'un nombre entier N est définie par récurrence, de la manière suivante :

u₀ = N

et pour tout entier  :

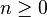
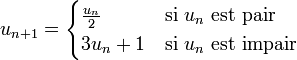
La conjecture affirme que, pour tout N > 0, il existe un indice n tel que u_n = 1.

L'observation graphique de la suite pour N = 15 et pour N = 127 montre que la suite peut s'élever assez haut avant de retomber. Les graphiques font penser à la chute chaotique d'un grêlon ou bien à la trajectoire d'une feuille emportée par le vent. De cette observation est né tout un vocabulaire imagé : on parlera du vol de la suite.

On définit alors :

• le temps de vol : c'est le plus petit indice n tel que u_n = 1

Il est de 17 pour la suite de Syracuse 15 et de 46 pour la suite de Syracuse 127

• le temps de vol en altitude : c'est le plus petit indice n tel que u_n+1 < u₀

Il est de 10 pour la suite de Syracuse 15 et de 23 pour la suite de Syracuse 127

• l'altitude maximale : c'est la valeur maximale de la suite

Elle est de 160 pour la suite de Syracuse 15 et de 4372 pour la suite de Syracuse 127

Quelques résultats

Il existe des arguments heuristiques et statistiques de nature à motiver la conjecture : par exemple, considérons l'effet de l'opération de la suite de Syracuse compressée sur un nombre v assez grand : si v est pair, il est multiplié par (1/2), tandis qu'un nombre impair se trouve multiplié par (3/2) environ. Dans les deux cas, on vérifie que la parité du résultat est indépendante de celle de v, de sorte que statistiquement l'on peut dire que l'effet de deux opérations consécutives de la suite revient à multiplier le nombre de départ par (3/4), ou encore que l'opération de Syracuse est contractante, en moyenne, dans un rapport approximativement égal à la racine carrée de (3/4) = 0,866…

Ce rapport nettement inférieur à l'unité suggère fortement que les éléments successifs d'une suite de Syracuse ne peuvent croître indéfiniment. Il n'existe aucune preuve rigoureuse de cette affirmation. Également, l'argument ici esquissé n'exclut nullement l'existence de cycles non triviaux.

Concernant la répartition des nombres qui satisfont à l'hypothèse de Syracuse, par des méthodes élaborées de programmation linéaire on arrive à montrer que, pour x suffisamment grand, le nombre d'entiers inférieurs à x qui satisfont l'hypothèse de Syracuse est au moins x^a pour certaine constante a < 1. En 2002, I. Krasikov et J. Lagarias obtinrent a = 0,84 .

Une voie d'exploration intéressante consiste en l'étude systématique du comportement de la suite de Syracuse à l'aide d'ordinateurs, pour des nombres de départ de plus en plus grands. On a ainsi vérifié la conjecture pour tout N < 2⁶² (janvier 2008 - T. Oliveira e Silva.) La grandeur de ce nombre, supérieur à quatre milliards de milliards, est de nature à renforcer notre croyance en la vérité de la conjecture de Syracuse. Il convient cependant de comprendre qu'aussi loin que l'on poursuive le calcul, il ne peut directement fournir une démonstration de cette conjecture; le calcul pourrait éventuellement, au contraire, rencontrer un contre-exemple, qui démontrerait la fausseté de la conjecture. Cette approche présente aussi l'intérêt de fournir des résultats numériques utilisables par les théoriciens pour compléter leurs démonstrations. Par exemple, en utilisant la borne N ci-dessus avec un théorème sur la longueur des cycles de la suite de Syracuse, démontré par Matti K. Sinisalo, on peut conclure qu'à part le cycle trivial (1,4,2,1…) il n'existe aucun cycle de longueur inférieure à 17 milliards

Les résultats numériques permettent de chercher des corrélations entre le nombre de départ N et la durée de vol, ou le record d'altitude. On a ainsi observé que si les records d'altitude pouvaient être très élevés, la durée du vol était en comparaison plus modeste. Une observation sur les nombres déjà étudiés semble indiquer que l'altitude maximale est majorée par φ(N).N² où φ(N) pourrait être soit une constante, soit une fonction lentement croissante. Le temps de vol est plus erratique mais semble majoré par un multiple du logarithme de N. Les expériences numériques suggèrent ainsi de nouvelles conjectures auxquelles les théoriciens peuvent s'attaquer.

En revanche, la recherche théorique est seule en mesure d'apporter des lumières concernant l'existence de trajectoires infinies : il a été démontré que l'ensemble des nombres appartenant à une telle trajectoire aurait une densité asymptotique nulle; pour rester dans l'image du vol, on pourrait dire que le grêlon, pour ne pas retomber jusqu'au sol, doit acquérir et maintenir une haute « vitesse de libération ». Si la conjecture est vraie, alors un tel vol infini est impossible.

La relative faiblesse des résultats obtenus en dépit de l'application acharnée de méthodes mathématiques puissantes par des esprits brillants a conduit certains chercheurs à se demander si la conjecture de Syracuse pourrait être un problème indécidable. En 1972, John Conway établit l'indécidabilité algorithmique pour une famille de problèmes qui généralise de manière naturelle le problème 3x+1. Ce résultat implique qu'il y a dans la famille considérée des problèmes individuels qui sont indécidables, sans qu'on puisse dire lesquels, et ne résout pas la décidabilité du problème de Syracuse en particulier.