Variable aléatoire réelle - Définition

Introduction

Un exemple de variable aléatoire :
la fonction qui associe au résultat du jet de deux dés la somme de leurs valeurs

Une variable aléatoire réelle est une variable aléatoire à valeurs dans , ou une partie de  ; c'est une fonction définie depuis l'ensemble des résultats possibles d'une expérience aléatoire, dont on doit pouvoir déterminer la probabilité qu'elle prenne une valeur donnée ou un ensemble donné de valeurs. Les variables aléatoires réelles sont les variables aléatoires les plus couramment étudiées, ce qui conduit certains auteurs à omettre l'adjectif réel, et à parler de variable aléatoire tout court.

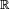
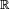
Les variables aléatoires sont très utilisées en théorie des probabilités et en statistiques. Dans les applications, les variables aléatoires sont utilisées pour modéliser le résultat d'un mécanisme non-déterministe ou encore comme le résultat d'une expérience non-déterministe qui génère un résultat aléatoire. En statistique mathématique ou inférentielle, les variables aléatoires servent généralement à modéliser des populations supposées infinies.

• L'article qui suit traite les variables aléatoires réelles

• L'article Variable aléatoire généralise cet article au cas non réel sous l'angle de la théorie de la mesure

• L'article Variables aléatoires élémentaires aborde la notion de variable aléatoire d'une manière plus intuitive

Détails

• À l'origine, une variable était une fonction de gain, qui représentait le gain obtenu à l'issue du résultat d'un jeu. Par exemple, supposons qu'un joueur lance un dé et que celui-ci gagne 1€ s'il amène un six et perde 10€ s'il amène un autre résultat. Alors il est possible de définir la variable aléatoire de gain qui associe 1 au résultat « six » et -10 à un résultat inintéressant. La probabilité pour que la variable aléatoire prenne la valeur 1 correspond exactement à la probabilité pour que le joueur gagne 1€.

• La variable aléatoire réelle la plus simple est donnée par le résultat d'un lancer au jeu de pile ou face, qui vaut pile ou face. Un autre exemple simple est donné par le résultat d'un jet de dés, pour lequel les valeurs possibles sont 1, 2, 3, 4, 5, 6 (si le dé est classiquement cubique). De telles variables aléatoires réelles sont qualifiées de discrètes car elles prennent des valeurs bien séparées. A contrario, la mesure de la taille d'un individu pris au hasard dans une population ressemble davantage à un nombre réel positif (cela n'est pas tout à fait vrai non plus, car des questions ergonomiques rendent d'autant plus improbable l'énoncé d'un nombre qu'il comporte de décimales significatives; l'attracteur est en fait un fractal). Cette variable aléatoire réelle est alors qualifiée par convention de continue. L'étude de la répartition des valeurs prises par une variable aléatoire conduit à la notion de loi de probabilité.

• En mathématiques, et plus précisément en théorie des probabilités, une variable aléatoire est une fonction mesurable définie sur un espace de probabilités. La mesure image correspondante est appelée loi de la variable aléatoire. Ce type de fonction permet de modéliser un phénomène aléatoire, comme par exemple le résultat d'un jet de dés. Une propriété intéressante de l'intégrale de Lebesgue fait qu'un évènement de probabilité strictement nulle n'est pas nécessairement impossible au sens strict du terme (ainsi, considérons un réel tiré au hasard dans l'intervalle [0, 1] ; la probabilité qu'il soit rationnel est nulle, alors que les rationnels constituent dans cet intervalle un ensemble infini, et même partout dense).