Copule (mathématiques) - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Aspects probabilistes des copules - Aspects statistiques - Quelques copules classiques

Introduction

En statistiques, une copule est un objet mathématique venant de la théorie des probabilités. La copule permet de caractériser la dépendance entre les différentes coordonnées d'une variable aléatoire à valeurs dans $\R^d$ sans se préoccuper de ses lois marginales.

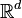
Aspects probabilistes des copules

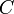
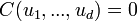
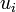
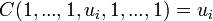
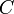
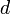
Une copule est une fonction de répartition, notée $\mathcal{}C$ , définie sur $\mathcal{}[0,1]^d$ dont les marges sont uniformes sur $\mathcal{}[0,1]$ . Une caractérisation est alors que $\mathcal{}C(u_1,...,u_d)=0$ si une des composantes $\mathcal{}u_i$ est nulle, $\mathcal{}C(1,...,1,u_i,1,...,1)=u_i$ , et $\mathcal{}C$ est $\mathcal{}d$ - croissante.

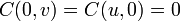
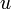
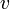
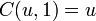
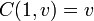
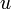
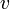
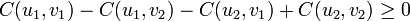
En dimension $2$ , $\mathcal{}C(0,v)=C(u,0)=0$ pour tout $\mathcal{}u$ et $\mathcal{}v$ , $\mathcal{}C(u,1)=u$ et $\mathcal{}C(1,v)=v$ , pour tout $\mathcal{}u$ et $\mathcal{}v$ , et enfin, la propriété de $2$ croissante se traduit par $\mathcal{}C(u_1,v_1)-C(u_1,v_2)-C(u_2,v_1)+C(u_2,v_2)\geq0$ .

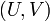
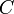
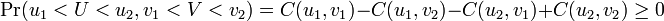
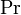
L'interprétation de cette notion de croissance se fait en notant que si $\mathcal{}(U,V)$ admet pour fonction de répartition $\mathcal{}C$ , $\mathcal{}\Pr(u_1<U<u_2,v_1<V<v_2)=C(u_1,v_1)-C(u_1,v_2)-C(u_2,v_1)+C(u_2,v_2)\geq0$ , la mesure $\mathcal{}\Pr$ étant nécessairement positive.

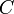
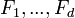
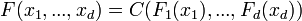
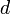
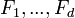
Le théorème de Sklar dit que si $\mathcal{}C$ est une copule, et si $\mathcal{}F_1,...,F_d$ sont des fonctions de répartition (univariées), alors $\mathcal{}F(x_1,...,x_d)=C(F_1(x_1),...,F_d(x_d))$ est une fonction de répartition de dimension $\mathcal{}d$ , dont les marges sont précisément $\mathcal{}F_1,...,F_d$ .

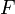
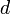
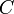
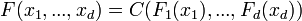
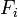
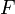
Et réciproquement, si $\mathcal{}F$ est une fonction de répartition en dimension $\mathcal{}d$ , il existe une copule $\mathcal{}C$ telle que $\mathcal{}F(x_1,...,x_d)=C(F_1(x_1),...,F_d(x_d))$ , où les $\mathcal{}F_i$ sont les lois marginales de $\mathcal{}F$ .

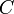
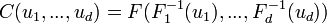
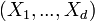
Si ces lois marginales sont toutes continues, la copule $\mathcal{}C$ est alors unique, et donnée par la relation $\mathcal{}C(u_1,...,u_d)=F(F_1^{-1} (u_1),...,F_d^{-1} (u_d))$ . Dans ce cas, on pourra alors parler de la copule associée à un vecteur aléatoire $\mathcal{}(X_1,...,X_d)$ .

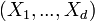
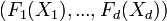
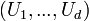
La copule d'un vecteur aléatoire $\mathcal{}(X_1,...,X_d)$ est alors la fonction de répartition du vecteur aléatoire $\mathcal{}(F_1(X_1),...,F_d(X_d))$ , que l'on notera parfois $\mathcal{}(U_1,...,U_d)$ .

Aspects statistiques

D'un point de vue statistique, les copules apparaissent naturelles comme la distribution des rangs.

Les copules apparaissent dans les espaces métriques de probabilité ou en logique floue (fuzzy logic).

Liens externes

Quelques copules classiques

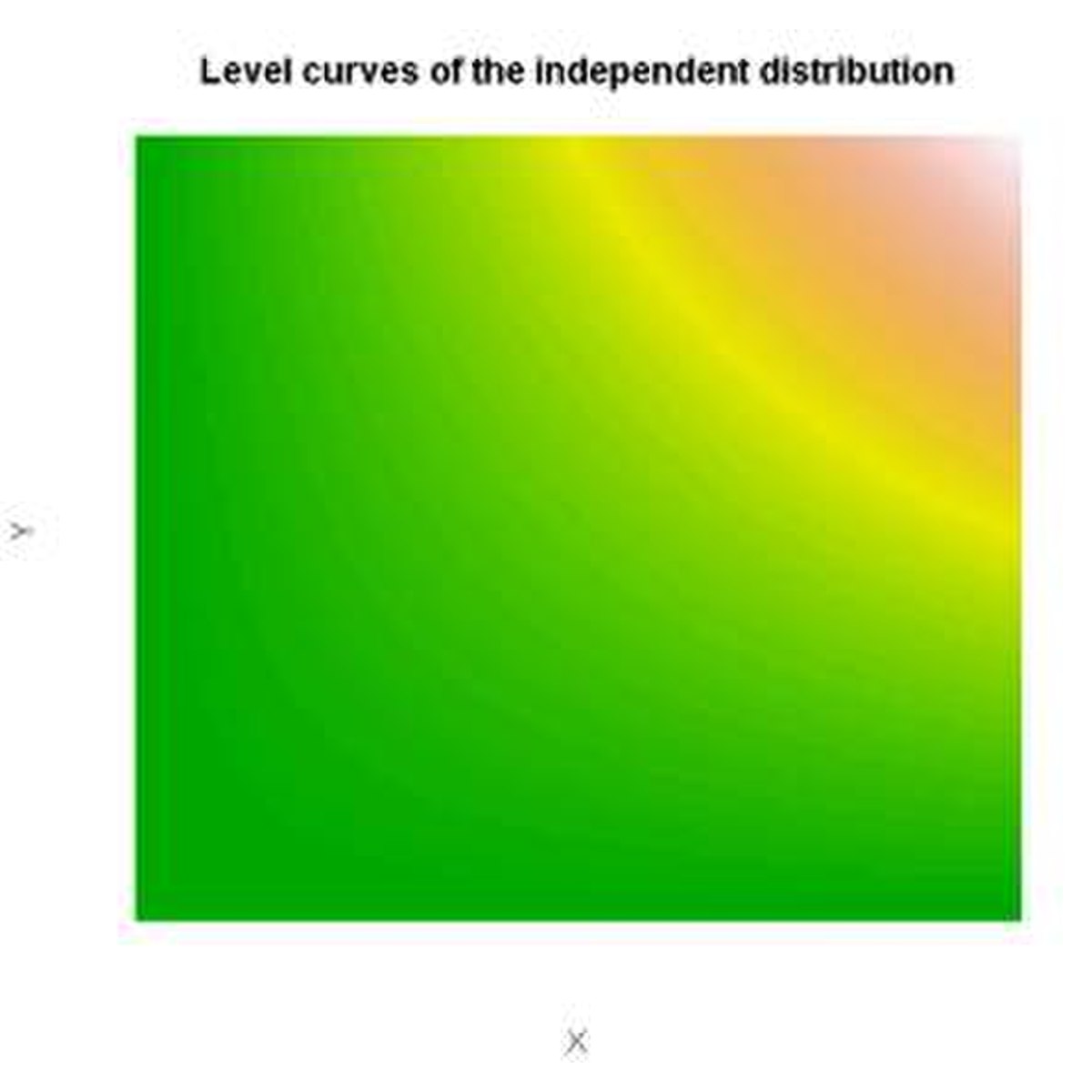
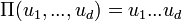
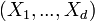
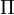
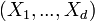
Parmi les copules usuelles, la copule produit $\mathcal{}\Pi(u_1,...,u_d)=u_1...u_d$ (on parlera aussi de copule indépendante). $\mathcal{}(X_1,...,X_d)$ a des composantes indépendantes si et seulement si $\mathcal{}\Pi$ est une copule du vecteur $\mathcal{}(X_1,...,X_d)$ .

Cop-indep-3d.jpg

Copule indépendante

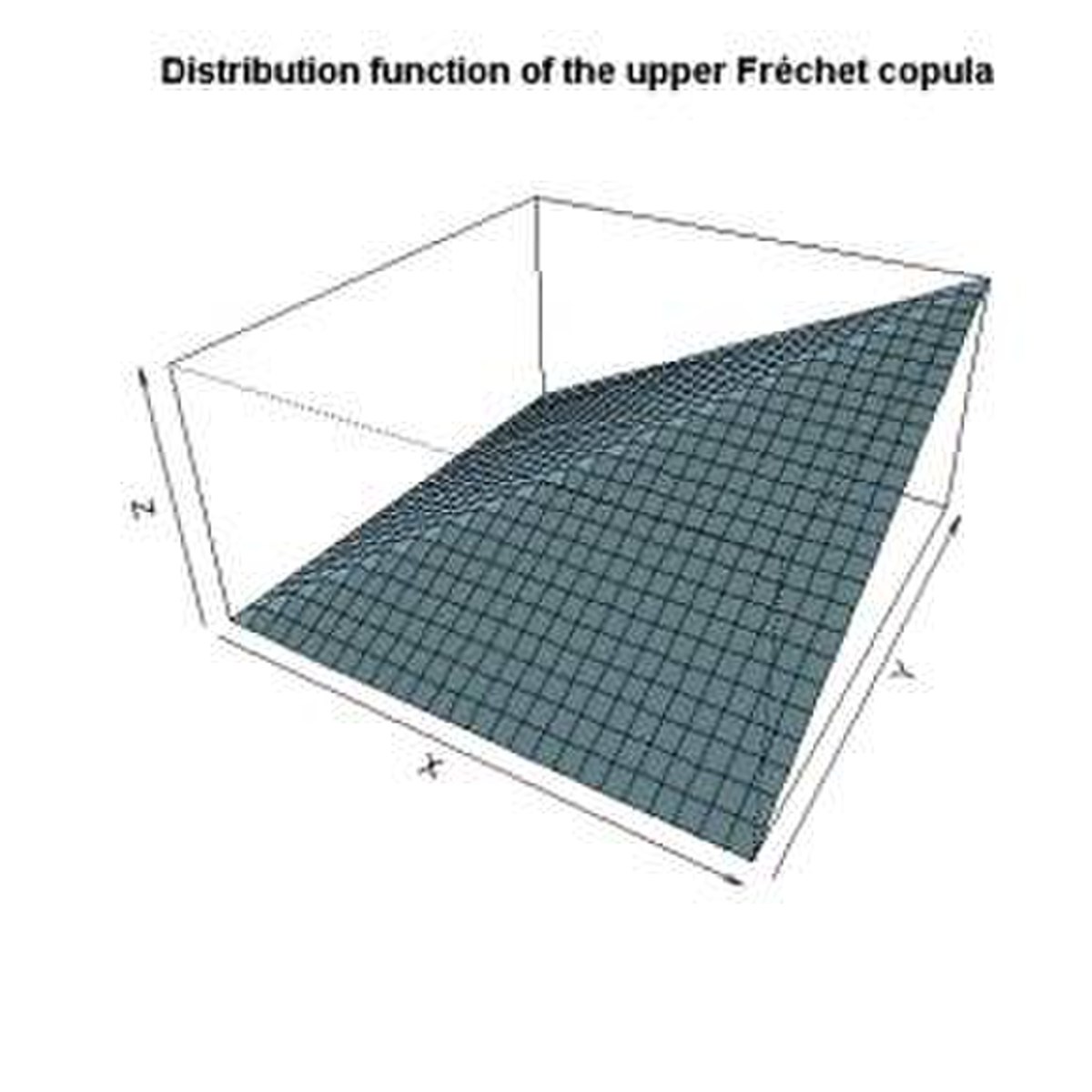
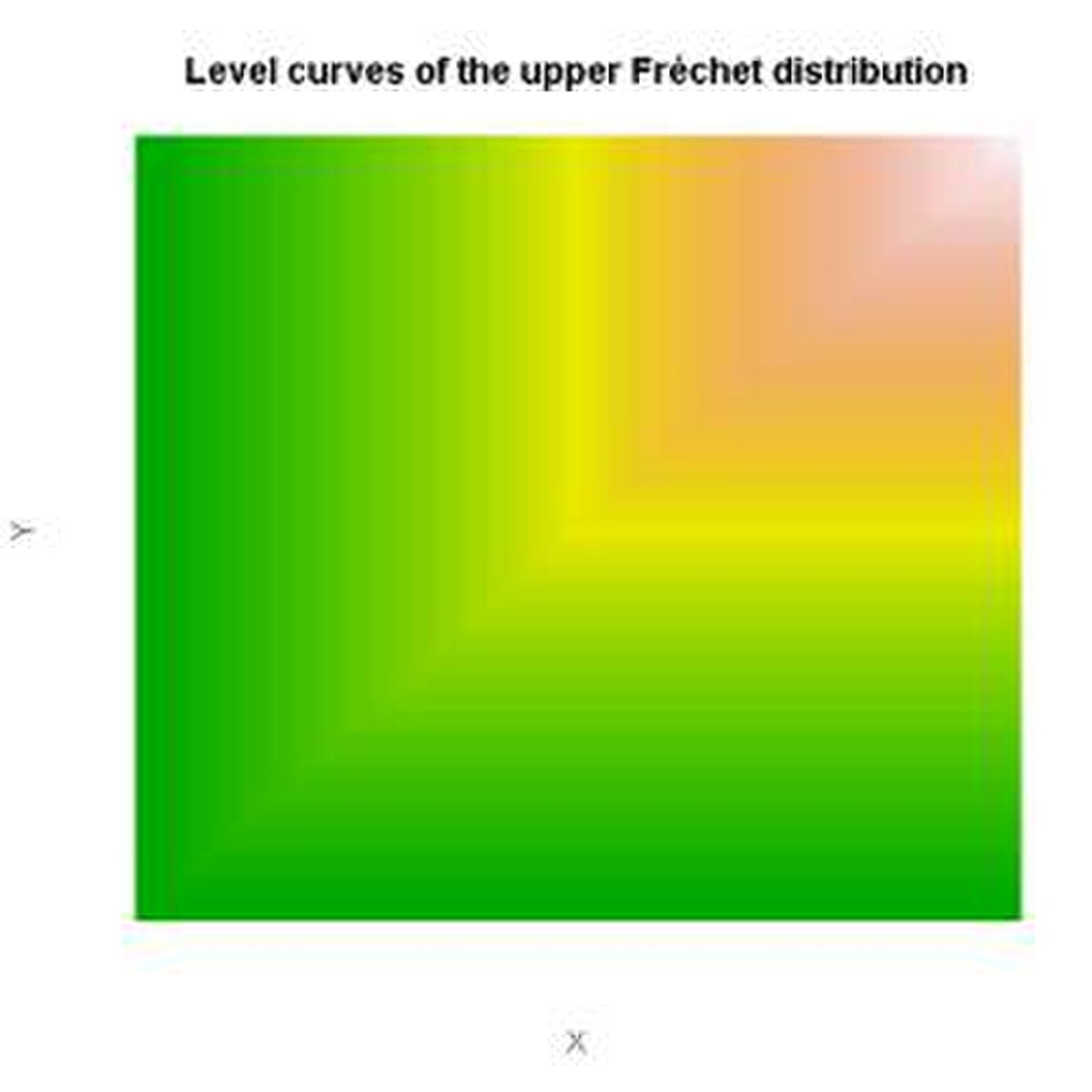
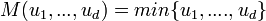
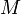
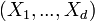
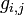
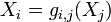
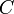
La copule comonotone, ou copule du minimum, est définie par $\mathcal{}M(u_1,...,u_d)=min\{u_1,....,u_d\}$ . $\mathcal{}M$ est une copule du vecteur $\mathcal{}(X_1,...,X_d)$ si et seulement s'il existe des transformations croissantes $\mathcal{}g_{i,j}$ telles que $\mathcal{}X_i=g_{i,j}(X_j)$ . 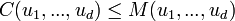Cette copule correspond à la borne supérieur de Fréchet-Hoeffding, au sens où pour toute copule $\mathcal{}C$ , $C(u_1,...,u_d)\leq M(u_1,...,u_d)$ .

Copule comonotone

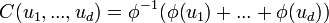
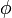
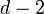
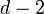
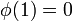
Une classe particulièrement importante de copule est celle des copules Archimédiennes, définies par $\mathcal{}C(u_1,...,u_d)=\phi^{-1}(\phi(u_1)+...+\phi(u_d))$ , où $\mathcal{}\phi$ (appelé générateur de la copule Archimédienne) est au moins $\mathcal{}d-2$ fois continument dérivable, dont la dérivé $\mathcal{}d-2$ est décroissante convexe, et telle que $\mathcal{}\phi(1)=0$ .

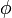
Ce générateur est unique à une constante (positive) multplicative près. Une sous classe relativement large est obtenue lorsque $\mathcal{}\phi$ est l'inverse d'une transformée de Laplace (et une interprétation factorielle est alors possible). Parmi les cas particuliers,

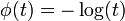
la copule indépendante obtenue lorsque $\mathcal{} \phi(t) = -\log(t)$ ,

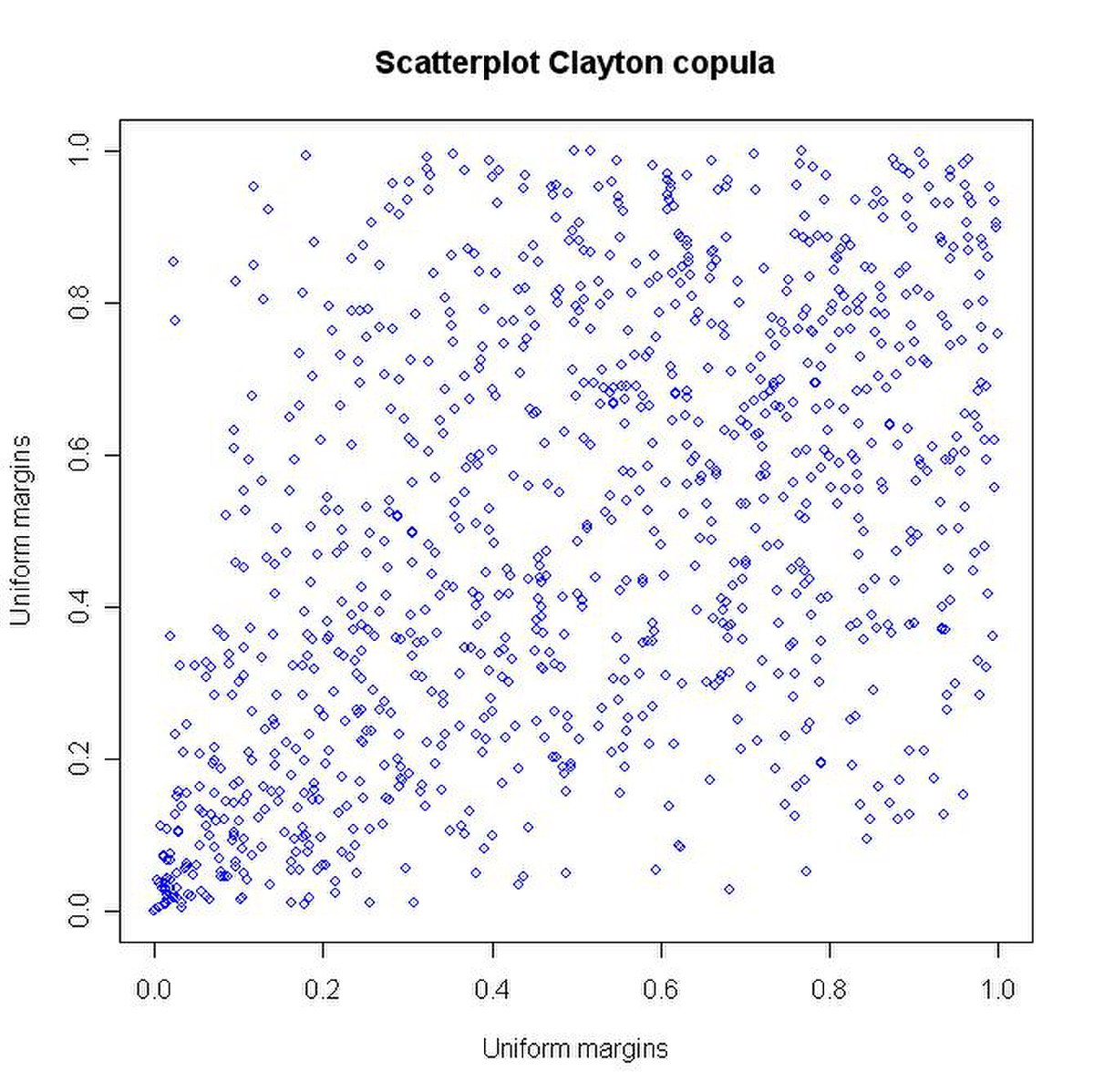
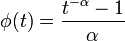
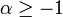
la copule de Clayton obtenue lorsque $\mathcal{} \phi(t) = \frac{t^{-\alpha}-1}{\alpha}$ , avec $\mathcal{}\alpha\geq -1$ . Le générateur est alors l'inverse de la transformée de Laplace de la loi Gamma. Cette copule est la seule copule Archimédienne invariante par troncature,

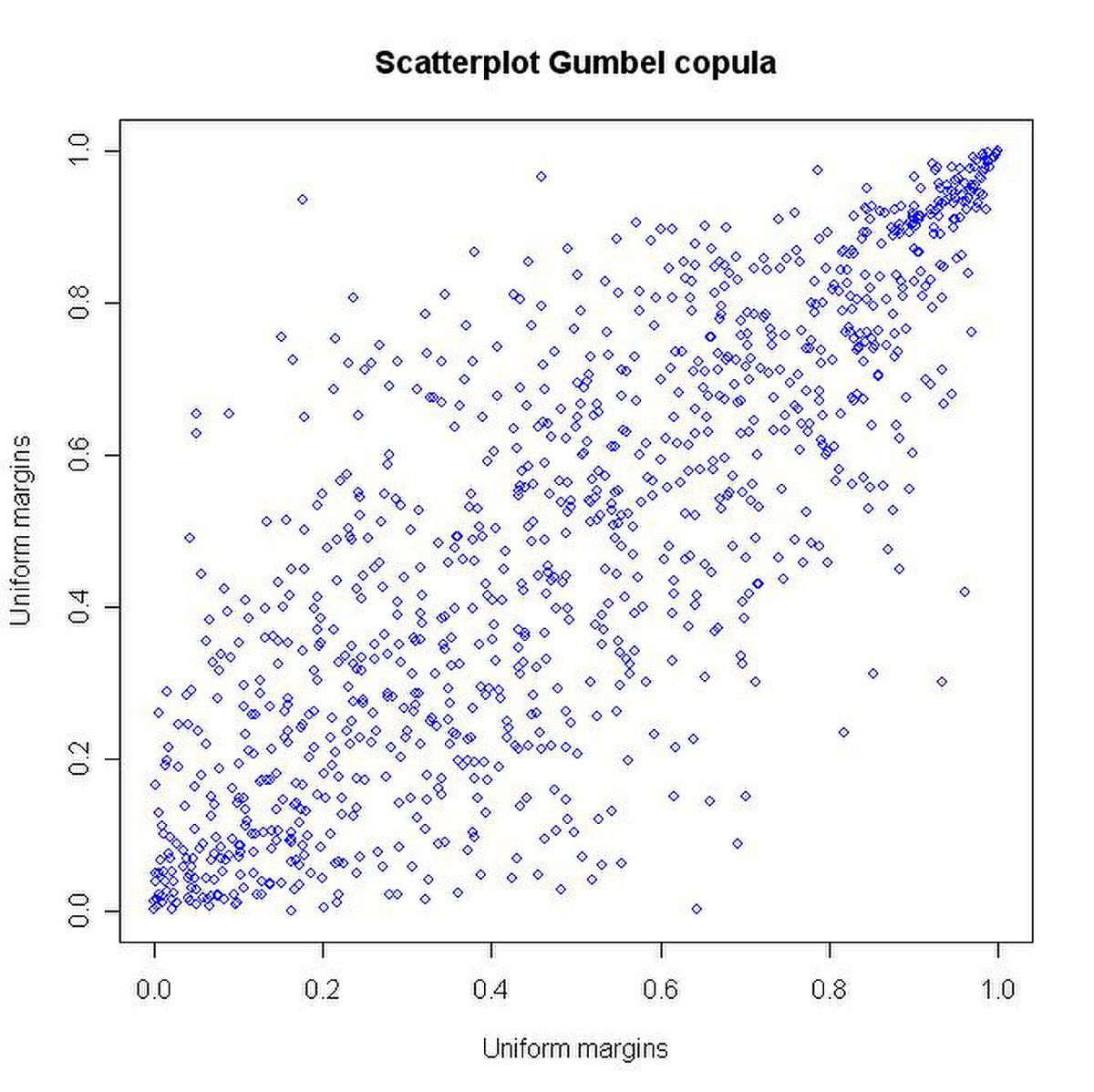
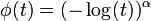
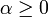
la copule de Gumbel obtenue lorsque $\mathcal{} \phi(t) = (-\log(t)) ^\alpha$ , avec $\mathcal{}\alpha\geq 0$ .

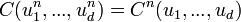
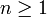
Le générateur est alors l'inverse de la transformée de Laplace de la loi stable. Cette copule est la seule copule Archimédienne vérifiant une propriété de max-stabilité, c’est-à-dire $\mathcal{}C(u^n_1,...,u^n_d)=C^n(u_1,...,u_d)$ , pour tout $\mathcal{}n\geq 1$ ,

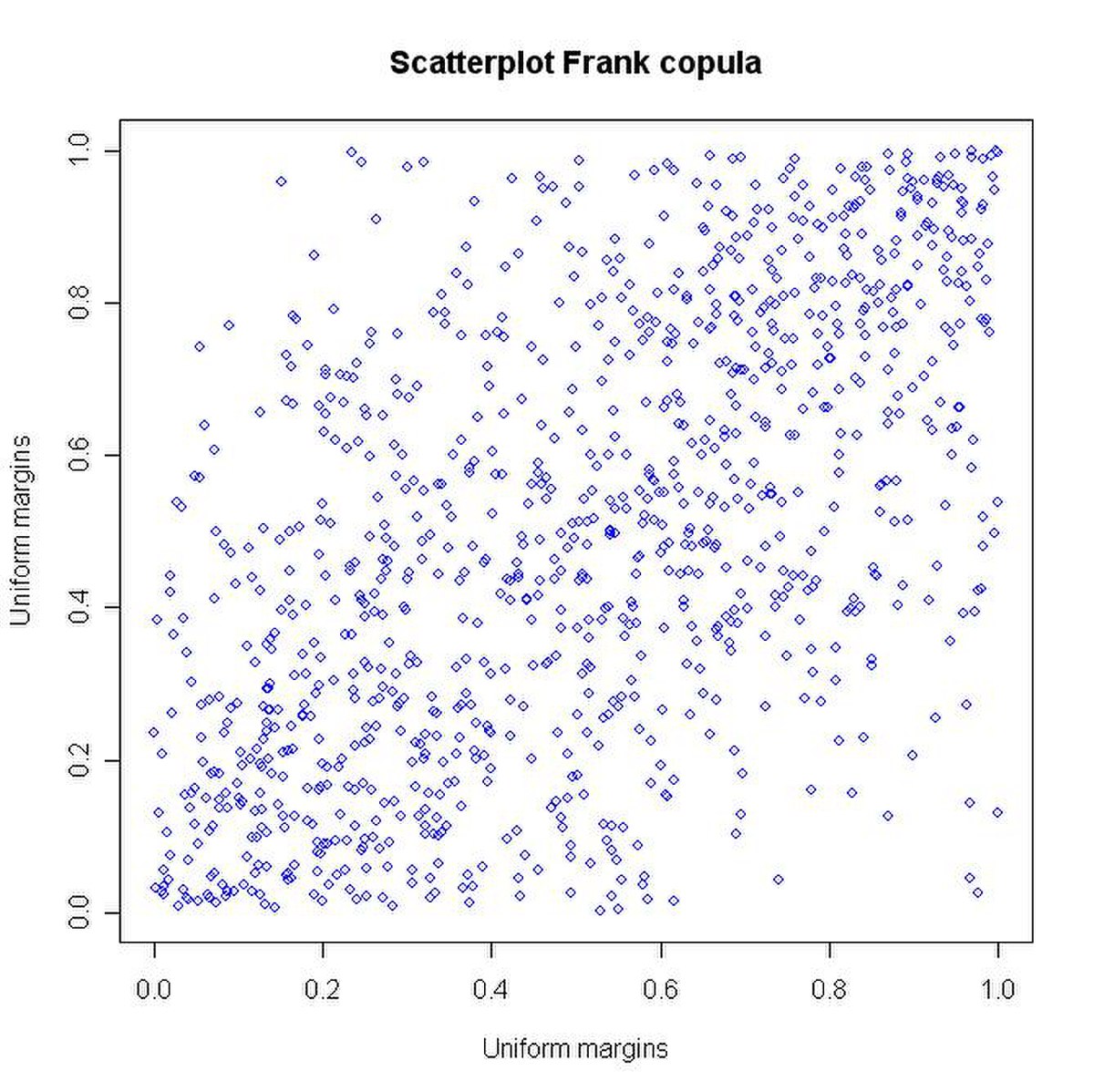
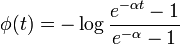
la copule de Frank obtenue lorsque $\mathcal{} \phi(t) = -\log\frac{e^{-\alpha t}-1 }{e^{-\alpha }-1 }$ . Cette copule est la seule qui soit symétrique dans la queue inférieure et supérieure,

Cop-Frank-density.JPG

Copule de Frank

Cop-Clayton-density.JPG

Copule de Clayton

Cop-Gumbel-density.JPG

Copule de Gumbel

Copule de Frank

Copule de Clayton

Copule de Gumbel

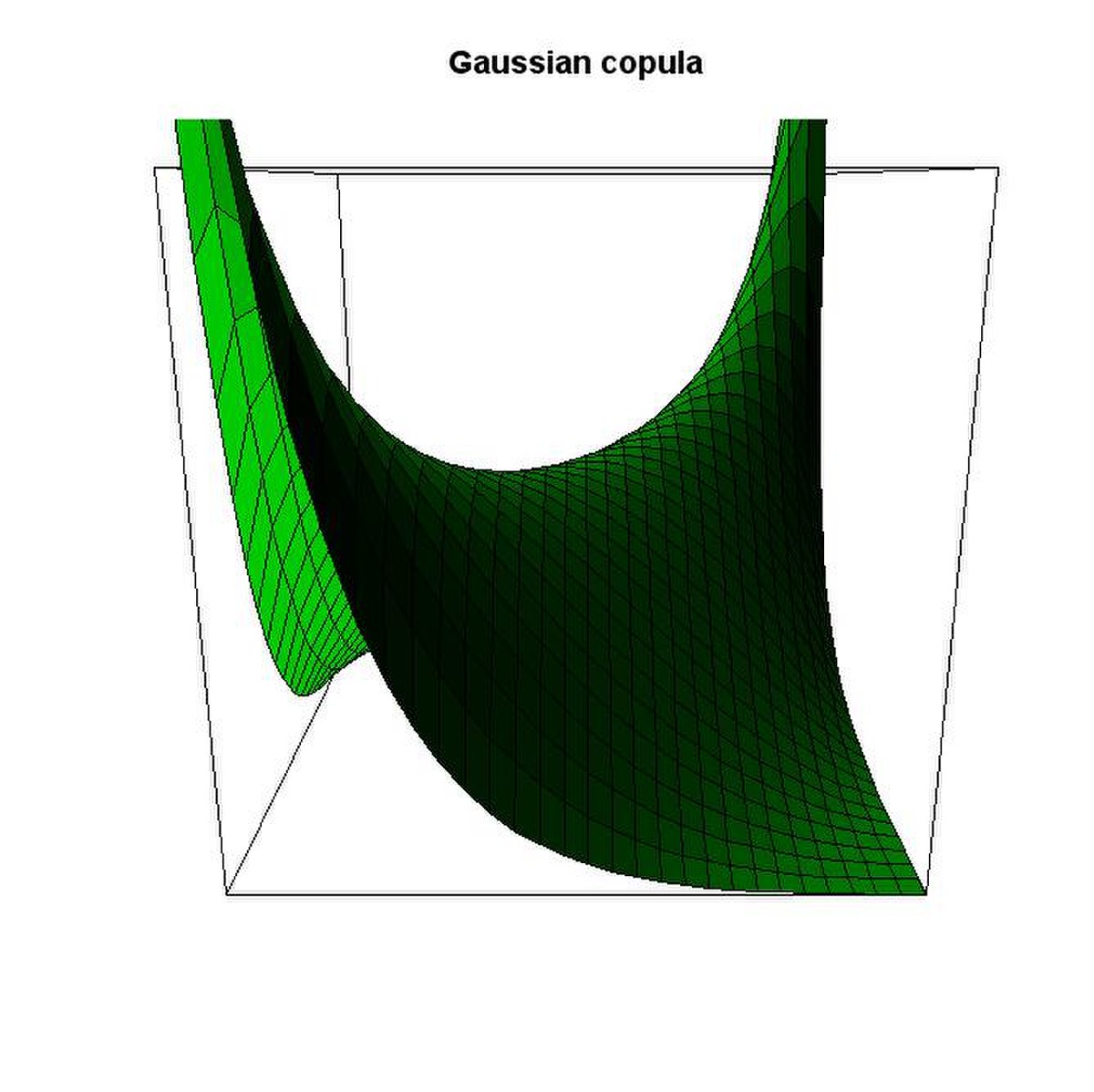
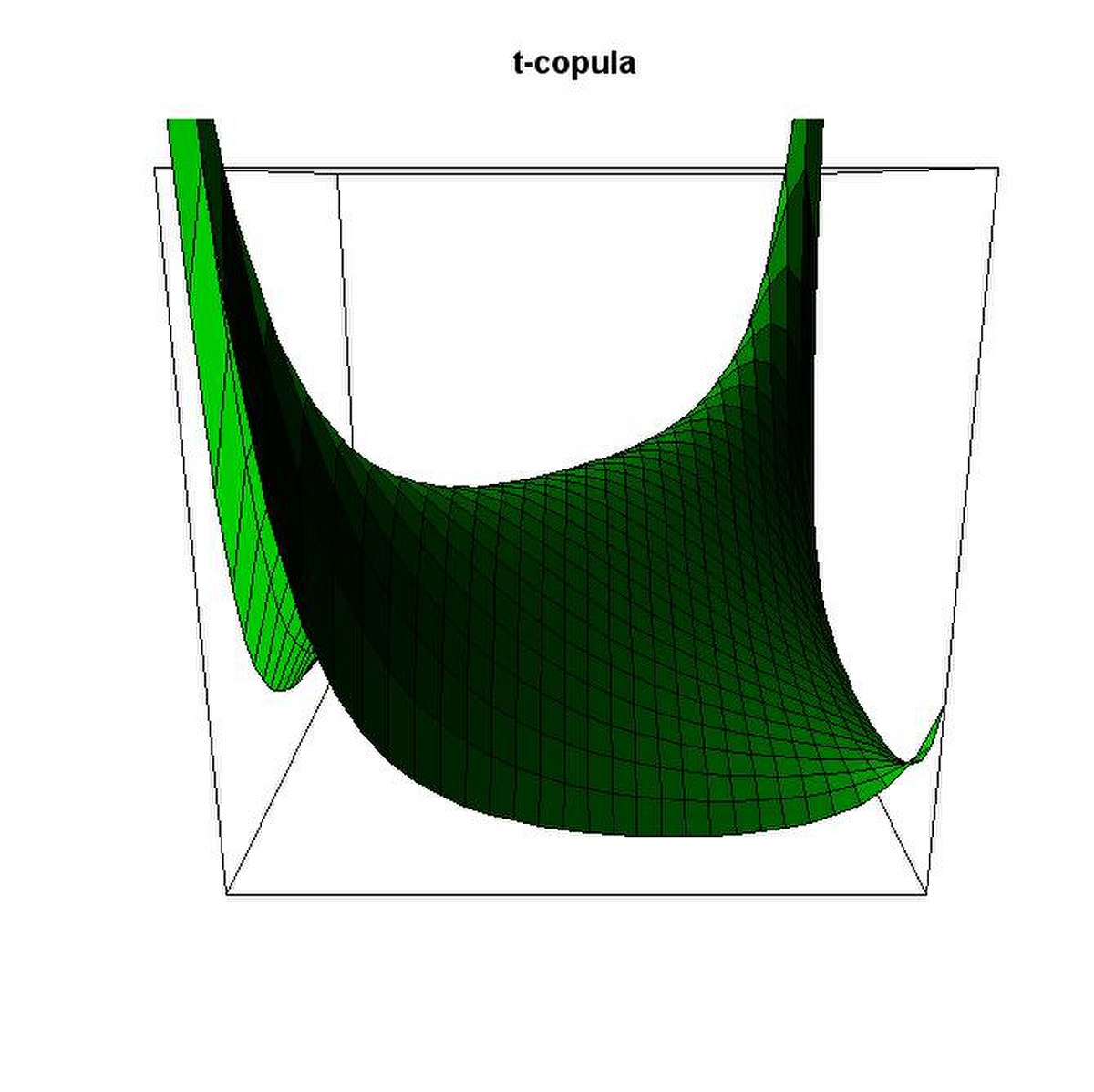
Les copules elliptiques...

Copule Gaussienne

Copule de Student (t)

- Introduction - Aspects probabilistes des copules - Aspects statistiques - Quelques copules classiques

Le télescope James Webb, poussé à ses limites, découvre ces structures incroyablement anciennes 🔭

Le rôle surprenant de la grossesse contre la grippe A 🦠

Découverte d'une nouvelle espèce éteinte grâce à... un accélérateur de particules ⚛️

Une avancée prometteuse pour le déploiement des batteries sodium-ion 🔋

Voici comment et pourquoi le risque de cancer augmente... puis diminue avec l'âge 🧬

Le Soleil bientôt en "zone de combat": une période de turbulences extrêmes ☀️

Les rhumatismes plus douloureux par temps humide: vrai ou faux ? 🌧️

Ce nouveau type de moteur repousse les limites du vol supersonique ✈️

Poster sur les réseaux sociaux peut nuire à votre santé mentale 🧠

Une super-Terre entre Mars et Jupiter ? 🌎

Découverte impressionnante d'un fossile de crocodile géant 🐊

Cet accident en laboratoire pourrait transformer drastiquement la mémoire numérique ⚡

Un virage technologique révèle l'impact du diabète gestationnel 🩺

Insolite: ces loups butinent des fleurs ! Des grands carnivores pollinisateurs ? 🌼

Ce fin gilet robotisé soulage les tâches répétitives 🦾

Les équations d'Einstein invalidées ? 👀

Ce tatouage électronique se connecte à votre cerveau 🧠

Cette IA de Google prédit la météo mieux que jamais, et sur 15 jours ! 🌦️

Des plats au bœuf... sans bœuf ? 🥩

Ce moteur de recherche d'un nouveau genre bouscule nos habitudes 🔍

Pourquoi les cheveux bouclent-ils en fonction de la météo ? 🌦️

Découverte: d'autres univers plus propices à la vie que le notre 👽

Ces sons urbains qui minent notre santé mentale 🚗

La testostérone impacte-t-elle vraiment le désir sexuel des hommes ? 🔥

Des microalgues éliminent les métaux lourds: voici comment 🧪

Et voici un qubit mécanique ! 🖥️

Les lentilles de contact sont-elles vraiment sans danger ? 👁️

Dans la course à l'IA générative, Google lance son générateur de vidéos 🎥

Une zone oubliée du cerveau permet aux paralysés de marcher à nouveau 🧠

Cette astuce quotidienne ajoute 11 ans à votre vie 🕒

Révolutions, migrations des européens... les éruptions volcaniques ont influencé l'histoire 🌋

Soit l'énergie noire n'est pas constante, soit une seconde force inconnue est à l'œuvre... 🌀

Voici pourquoi l'alcool peut rendre agressif 🥂

Expérience inédite: ce laser projette une ombre visible 💥

Ce plat millénaire réduit significativement la graisse corporelle 🍽️

Les scientifiques trompés ? La Voie Lactée n'est PAS comme les autres galaxies 🔭

Pourquoi ce que pensent les autres de nous nous fait tant ruminer ? 🧠

De la vie découverte sur un échantillon de l'astéroïde Ryugu (oups) 👽

Des anomalies incompréhensibles de températures détectées simultanément presque partout sur Terre 🌡️

Cette planète, trop jeune pour exister, bouscule les lois de l'astronomie 🪐

Une montagne d'or découverte en Chine ⛏️

Cette simulation de l'Univers est totalement vertigineuse 🌀

Une pilule pourrait-elle imiter les bienfaits du yoga ? 🧘

Nous serions-nous trompés sur l'origine de l'écriture alphabétique ? ✍️

Voici pourquoi votre enfant triche et ce que cela révèle 🧠

Le Sahara verdit, et cela pourrait bien (re)changer notre climat 🌱

Neuralink: un bras robotique contrôlé par la pensée 🦾

Ces fossiles humains à grands crânes seraient-ils une espèce jusqu'alors inconnue ? 💀

L'étonnant impact du froid sur notre sommeil ❄️

Une base cachée de missiles nucléaires repérée par erreur sous la calotte glacière ☢️

Page générée en 0.503 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales | Partenaire: HD-Numérique
Version anglaise | Version allemande | Version espagnole | Version portugaise