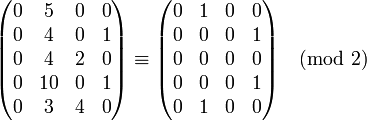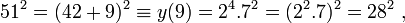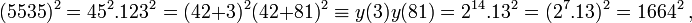Crible quadratique - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Objectif de base - Polynômes multiples - Optimisation de la recherche de congruences - Records de factorisation - Exemple

Records de factorisation

Jusqu'à la découverte du crible généralisé sur les corps de nombres, l'algorithme non spécialisé le plus rapide (asymptotiquement) que l'on connaissait était le crible quadratique. À présent, la méthode des courbes elliptiques possède le même temps d'exécution asymptotique que le crible quadratique (dans le cas où n est produit de deux grands nombres premiers), mais dans la pratique, le crible quadratique est plus rapide car il utilise des calculs en simple précision au lieu des calculs en multi-précision utilisés par la méthode des courbes elliptiques.

Le 2 avril 1994, la factorisation de RSA-129 fut achevée à l'aide du crible quadratique. C'est un nombre de 129 chiffres, produit de deux grands nombres premiers, l'un de 64 chiffres et l'autre de 65. La base des facteurs pour cette factorisation contenait 524 339 nombres premiers. La collecte des données prit 5 000 années MIPS faite par calcul distribué via Internet. Les données collectées totalisèrent 2 Go. La phase d'exploitation des données prit 45 heures sur le supercalculateur MasPar (en) (massivement parallèle) de Bellcore (devenu depuis Telcordia Technologies (en)). Ce fut, parmi les records publiés, le plus grand nombre factorisé par un algorithme non spécialisé, jusqu'à ce que le crible sur les corps de nombres soit utilisé pour la factorisation de RSA-130, terminée le 10 avril 1996. Tous les nombres RSA factorisés depuis l'ont été par le crible sur les corps de nombres.

Le record suivant du crible quadratique est la décomposition, en 2001, d'un nombre de 135 chiffres en produit de deux facteurs premiers, l'un de 66 chiffres et l'autre de 69. (Ce produit est un diviseur du nombre $2803 - 2 402 + 1$ , qui est lui-même un facteur aurifeuillien (en) de $21606 + 1$ .)

Exemple

Voici un exemple. Soit n = 1817. La partie entière de sa racine carrée est 42. Comme n est petit, le polynôme y(z) = (42+z)²-1817 suffit (pas besoin du crible multipolynomial).

Collecte des données

On se limite, comme base F de facteurs, à -1 et aux nombres premiers p pour lesquels n est un résidu quadratique modulo p :

F = { - 1,2,7,13}.

Puisque F compte 4 éléments, on a besoin de 5 couples réguliers (z, y(z)). Les premiers trouvés (par ordre croissant sur z) sont les suivants :

z	y(z)=(42+z)²-1817	factorisation de y(z)
1	32	−1⁰ • 2⁵ • 7⁰ • 13⁰
3	208	−1⁰ • 2⁴ • 7⁰ • 13¹
9	784	−1⁰ • 2⁴ • 7² • 13⁰
81	13312	−1⁰ • 2¹⁰ • 7⁰ • 13¹
103	19208	−1⁰ • 2³ • 7⁴ • 13⁰

(on pourrait aussi choisir des z négatifs).

Exploitation des données

On forme la matrice des exposants qui interviennent dans la factorisations des y(z) :

\begin{pmatrix} 0 & 5 & 0 & 0 \\ 0 & 4 & 0 & 1 \\ 0 & 4 & 2 & 0 \\ 0 & 10 & 0 & 1 \\ 0 & 3 & 4 & 0 \\ \end{pmatrix}\equiv\begin{pmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ \end{pmatrix}\pmod{2}

La troisième ligne (qui correspond à (z, y) = (9, 784)) est nulle modulo 2 donc est déjà une congruence de carrés, qu'on peut utiliser pour factoriser n : modulo 1817,

et pgcd(51+28,1817) = 79, pgcd(51-28,1817) = 23. Ce sont les deux facteurs non triviaux de 1817.

On aurait pu utiliser d'autres congruences de carrés déduites de cette matrice. Par exemple en combinant la deuxième ligne et la quatrième (puisque leur somme est paire) :

et pgcd(5535+1664,1817)=23, pgcd(5535-1664,1817)=79.

Cet exemple montre aussi que le crible quadratique n'est utile que pour n grand. Pour un nombre aussi petit que 1817, cet algorithme est un canon pour tuer une mouche. Les essais de divisions pourraient trouver un facteur en 9 divisions.