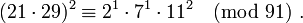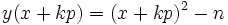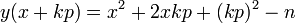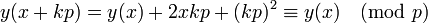Crible quadratique - Définition

Introduction

L'algorithme du crible quadratique est un algorithme de factorisation fondé sur l'arithmétique modulaire. C'est en pratique le plus rapide après le crible généralisé sur les corps de nombres, lequel est cependant bien plus compliqué, et n'est plus performant que pour factoriser un nombre entier d'au moins cent chiffres décimaux. Le crible quadratique est un algorithme de factorisation non spécialisé, c'est-à-dire que son temps d'exécution dépend uniquement de la taille de l'entier à factoriser, et non de propriétés particulières de celui-ci.

Objectif de base

L'algorithme, mis au point en 1981 par Carl Pomerance, est un raffinement de la méthode de factorisation de Dixon, elle-même basée sur celle de Fermat : on essaye d'établir une congruence de carrés modulo n (l'entier à factoriser), qui, souvent, conduit bien à une factorisation de n.

L'algorithme fonctionne en deux phases :

• la phase de collecte des données, où il collecte les informations qui peuvent conduire à une congruence de carrés, et
• la phase d'exploitation des données, où il place toutes les données qu'il a collectées dans une matrice et la résout pour obtenir une congruence de carrés.

La phase de collecte peut se paralléliser facilement et efficacement, mais pas la phase d'exploitation, à moins d'avoir peu de sous-systèmes et que chacun d'eux dispose d'une mémoire suffisante pour stocker toute la matrice (dans ce cas on peut utiliser l'algorithme par blocs de Wiedemann (en)).

L'approche naïve pour trouver une congruence de carrés est de choisir un nombre au hasard, l'élever au carré, et espérer que le plus petit reste (positif ou nul) modulo n soit un carré parfait (i.e. soit le carré d'un entier). Par exemple, modulo 5959, l'entier 80² est congru à 441=21². Pour n grand, cette approche trouve rarement une congruence de carrés, mais lorsque cela arrive, cette congruence est le plus souvent non triviale donc permet de factoriser n.

La durée d'exécution du crible quadratique pour factoriser un entier n est en

avec la notation O de Landau et la notation L (en).

Polynômes multiples

Dans la pratique, le seul polynôme y(x) = x² − n ne fournit pas suffisamment de (x, y) réguliers sur la base des facteurs. On utilise alors toute une famille de polynômes qui, pour être des carrés modulo n, doivent être d'une forme similaire à l'original :

Cette approche, appelée crible quadratique à polynômes multiples, est parfaitement adaptée à la parallélisation.

Optimisation de la recherche de congruences

Le crible quadratique essaie de trouver des couples d'entiers x et y(x) (où y(x) est une fonction de x) satisfaisant une condition bien plus faible que x² ≡ y² (mod n). Il choisit un ensemble de nombres premiers qu'on appelle base de facteurs, et cherche des x pour lesquels le "plus petit reste absolu" y(x) de x² modulo n se factorise complètement sur cette "base". De tels couples d'entiers sont dits réguliers relativement à cette base, et la factorisation de y(x) sur la base, jointe à la valeur de x, constitue ce qu'on appelle une relation. Le crible quadratique accélère le processus de recherche de relations en prenant x proche de la racine carrée de n. Ainsi y(x) sera plus petit, et aura donc plus de chance d'être "régulier". Pour x=[√n]+z avec z entier "petit",

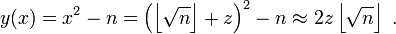
Néanmoins, cela implique aussi que y croît linéairement avec z.

Une autre façon d'augmenter les chances de régularité est d'augmenter simplement la taille de la base, mais cela impose de collecter plus de relations. En effet, pour être sûrs que les relations sont linéairement dépendantes, il faut qu'il y en ait au moins une de plus que le nombre de facteurs premiers dans la base.

Relations partielles et cycles

Même si, dans une relation, y(x) n'est pas régulier, il peut arriver qu'en fusionnant deux telles relations partielles on en forme une "complète". Il faut pour cela qu'en dehors de la base, les facteurs premiers des deux y soient les mêmes. Par exemple, si la base est {2, 3, 5, 7} et n = 91, en faisant le produit des deux relations partielles

et

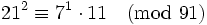
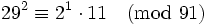
on obtient

On en déduit une relation complète en multipliant les deux côtés par le carré de 11^-1 modulo 91, c'est-à-dire de 58 (valeur obtenue à l'aide de l'algorithme d'Euclide étendu, par exemple) :

soit

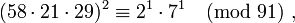
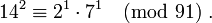
Une telle relation complète (obtenue par combinaison de relations partielles) est appelée un cycle. Quelquefois, la formation d'un cycle à partir de deux relations partielles conduit directement à une congruence de carrés, mais rarement.

Vérifier la régularité par criblage

Il existe plusieurs manières de vérifier la régularité des y. La plus évidente est la méthode des essais de divisions, bien que ceci augmente le temps d'exécution pour la phase de collecte des données. Une autre méthode parfois utilisée est la méthode des courbes elliptiques. Mais la pratique la plus courante est de procéder par criblage.

Ansi, si l'on connait un x tel que y(x) ≡ 0 (mod p), on en déduit toute une suite de y qui sont divisibles par p. En répétant ce processus pour d'autres valeurs de p, on trouve des valeurs régulières, par un processus de criblage (analogue au crible d'Ératosthène) au lieu d'avoir à tester la régularité à chaque fois (ce test systématique prendrait trop de temps pour de grands nombres comme ceux des records de factorisation ci-dessous). Au cours de ce processus on perd l'information détaillée de la factorisation des y réguliers collectés, mais comme ils n'ont que de "petits" facteurs (ceux de la base), on peut la recalculer rapidement.