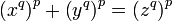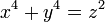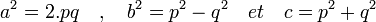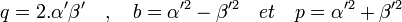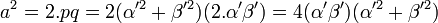Démonstrations du dernier théorème de Fermat - Définition

Introduction

Pierre de Fermat

En mathématiques, plus précisément en arithmétique modulaire, le grand théorème de Fermat traite des racines de l'équation diophantienne suivante, d'inconnues x, y et z :

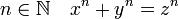
Il stipule qu'il n'existe aucune solution non triviale si le paramètre n est strictement supérieur à deux.

Une équation diophantienne est une équation à coefficients entiers dont les solutions recherchées sont entières. Si, à l'exemple de la question de l'article, l'expression est souvent simple, la résolution s'avère en général ardue.

En 1637 Pierre de Fermat propose cette équation et indique dans la marge de son exemplaire du livre Arithmetica de Diophante qu'il a trouvé une merveilleuse démonstration.

Il est peu probable qu'une démonstration accessible à Fermat existe. En effet, il fallut de nombreuses tentatives ainsi que près de 350 ans d'efforts pour qu'une preuve en soit donnée en 1994 par Andrew Wiles.

Généralités et cas élémentaires

Remarques

L'équation est homogène, c’est-à-dire que pour une valeur n donnée, si le triplet (x, y, z) est solution, alors (a.x, a.y, a.z) est aussi solution. En conséquence, les seules racines recherchées sont les triplets d'entiers premiers entre eux dans leur ensemble.

Si l'un des trois membres du triplet (x, y, z) est égal à zéro, alors l'équation devient évidente, de telles solutions sont dites triviales. L'objectif est donc la recherche de triplet solution tel que le produit x.y.z soit différent de zéro.

Si l'équation n'admet pas de solution pour une valeur p du paramètre, alors il n'existe pas de solution pour toute valeur n multiple de p. En effet, si l'on note n = p.q alors l'équation s'écrit:

En conséquence, les valeurs à traiter sont celles où n est un nombre premier. Il est toutefois à noter l'unique exception, correspondant au cas où n est égal à deux. En effet, des solutions existent, il est donc nécessaire d'étudier aussi le cas où n est égal à quatre.

Résultats sans appel à la théorie des nombres

Quelques résultats se démontrent sans structure complexe. Le cas où n est égal à deux, traité à la suite, est simple et date de l'antiquité. Celui où n est égal à quatre se démontre de manière un tout petit peu moins élémentaire. Les cas restant sont ceux où n est premier différent de deux. Il existe une démonstration qui n'utilise pas les entiers d'Eisenstein pour le cas où n est égal à trois, elle est néanmoins suffisamment astucieuse et difficile pour que le mathématicien Leonhard Euler ne propose qu'une démonstration inexacte.

Les autres cas sont techniques, l'utilisation d'entiers algébriques est indispensable. Le premier terme est bien une identité remarquable : xⁿ + yⁿ est en effet un multiple de x + y si n n'est pas une puissance de deux, cependant cette remarque est largement insuffisante pour conclure ne serait-ce que dans un cas.

Cas où n est égal à deux

Le théorème de Pythagore: a² + b² = c²

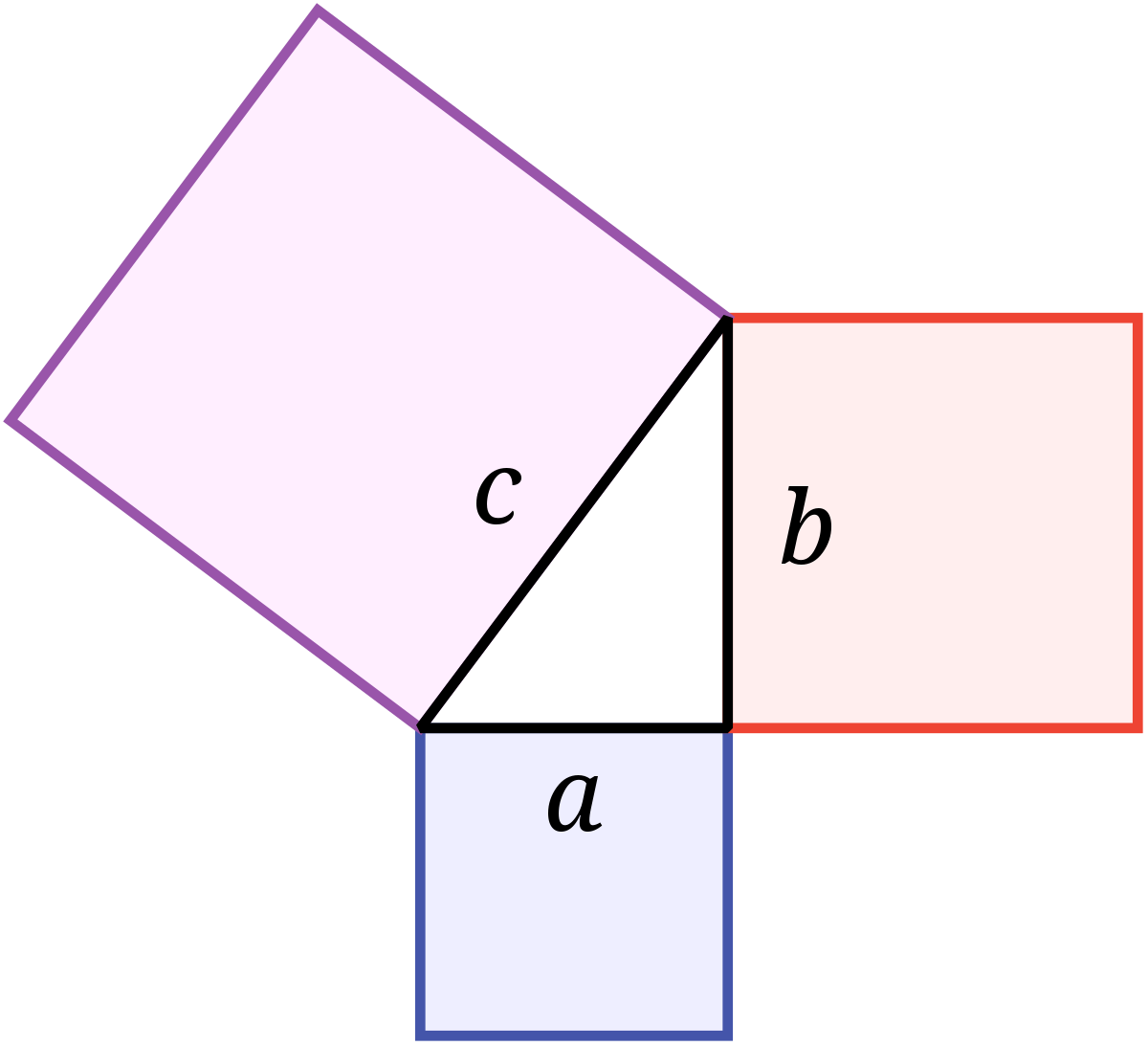
Le cas où n est égal à deux possède une interprétation géométrique. Il correspond aux longueurs entières des différents côtés d'un triangle rectangle.

Ce cas est connu depuis la haute antiquité. Ainsi, les sumériens connaissaient quelques exemples de solutions. La solution complète apparaît pour la première fois dans le livre X des Eléments d'Euclide vers 300 av. J.-C.

Ce cas est l'unique exception du théorème (si l'on omet le cas où n est égal à un). En effet, il existe des solutions non triviales si n est égal à deux : 3, 4 et 5 forment un triplet de solutions, appelé triplet pythagoricien. En conséquence, il devient important de considérer le cas n égal à quatre, pour démontrer qu'il n'existe pas d'autre puissance de deux admettant des solutions non triviales.

Une démonstration est donnée dans l'article Triplet pythagoricien.

Cas où n est égal à quatre

Ce cas est probablement l'unique traité par Fermat. Si aucune preuve écrite n'est trouvée dans sa correspondance, en revanche il démontre qu'il n'existe aucun triplet pythagoricien tel que x.y/2 soit un carré d'entier, ce qui s'exprime, dans le vocabulaire de l'auteur par l'aire d'un triangle rectangle ne peut être celle d'un carré. À partir de ce résultat, la démonstration est aisée. Pour cette raison, Fermat est très généralement considéré comme l'auteur de cette démonstration.

La méthode utilisée est celle de la descente infinie. La méthode consiste à trouver un autre triplet de solutions tel que le troisième entier est positif et strictement plus petit que celui de la solution initiale. Il est ainsi possible de descendre indéfiniment dans l'ensemble des entiers positifs, ce qui est contradictoire avec les propriétés de N.

Une preuve complète et nouvelle provient de Leonhard Euler , elle est aussi fondée sur la méthode de la descente infinie. Il en existe d'autres, par exemple utilisant la notion d'entiers de Gauss.