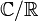Extension de corps - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, plus particulièrement en algèbre, l'extension d'un corps K est un corps L qui contient K comme sous-corps.
Par exemple,



On note parfois L / K pour indiquer que L est une extension de K.
Définition
Soit K un corps. Une extension de K est un couple (L, j) où L est un corps et j un morphisme de corps de K dans L (les morphismes de corps étant systématiquement injectifs).
On montre qu'il existe un sur-corps N de K et un isomorphisme de corps
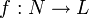
Une sous-extension de L / K est un sous-corps de L contenant K. Si V est un sous-ensemble de L, alors on définit le corps K(V) comme le plus petit sous-corps de L contenant K et V. Il est constitué des éléments de L pouvant être obtenus grâce à un nombre fini d'opérations additives et multiplicatives, et d'inversions sur K et V. Si L = K(V), on dit que L est engendré par V.
Extension transcendante
Une extension qui n'est pas algébrique est dite transcendante. Par exemple,
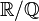
Extension transcendante pure
On dit que des éléments
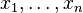
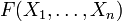
![K[T_1,\ldots, T_n]](https://static.techno-science.net/illustration/Definitions/autres/2/20496667b52257abfbda4b3696b1f9c5_c1a8958a690536809ee3e4056eb0c243.png)
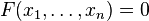
Si L est engendré par une famille d'éléments algébriquement indépendants sur K, l'extension est dite purement transcendante. Cela équivaut à dire que L est le corps des fractions d'un anneau de polynômes (à plusieurs ou même une infinité de variables) à coefficients dans K.
Toute extension est extension algébrique d'une extension purement transcendante.
Degré de transcendance
Une famille S d'éléments de L est appelée une base de transcendance si elle est algébriquement indépendante sur K et si elle n'est strictement contenue dans aucune famille algébriquement indépendante de L. Les bases de transcendance existent et ont toutes le même cardinal. Lorsque ce cardinal est fini, il est appelé le degré de transcendance de L sur K.
Extension de type fini
Une extension L/K engendrée par une famille finie V est dite de type fini. Toute extension finie est de type fini. L'extension
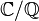
Extension algébrique
Si L est une extension de K, alors un élément de L qui est une racine d'un polynôme non-nul sur K est dit algébrique sur K. Dans le cas contraire, l'élément est dit transcendant sur K. Dans le cas où
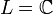
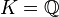
Si tout élément de L est algébrique sur K, l'extension L / K est dite algébrique.
Degré d'une extension
Si L / K est une extension de corps donnée, alors L est un espace vectoriel sur K, où l'addition vectorielle est l'addition dans L et la multiplication par un scalaire
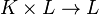

La dimension du K-espace vectoriel L est appelée le degré de l'extension et est notée
![\left[L:K\right]](https://static.techno-science.net/illustration/Definitions/autres/5/504685910e4ffadfcb54ee5281e32f86_ea5cbf031fc9da27cb93f581ce405766.png)
![\left[\mathbb C:\mathbb R\right]=2](https://static.techno-science.net/illustration/Definitions/autres/6/6df4fb4859037a3b98a97e7e1bb1fa90_f40b48238c00ebe788b9f8753af26d18.png)
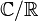


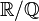
Si M est une extension finie de L qui est elle-même une extension finie de K, alors M est une extension finie de K et on a :
-
![\left[M:K\right]=\left[M:L\right]\cdot \left[L:K\right]](https://static.techno-science.net/illustration/Definitions/autres/7/767e79f8b40f584c8741faf769969661_47a7b45b54d611603faa8c6a6a5d51df.png)
Toute extension finie est algébrique, et toute extension algébrique est la réunion de ses sous-extensions finies.
Extension simple
Si L / K est une extension de corps et V est un sous-ensemble de L, alors on définit le corps K(V) comme le plus petit sous-corps de L contenant K et V. Il est constitué des éléments de L pouvant être obtenus grâce à un nombre fini d'opérations additives et multiplicatives, et d'inversions sur K et V. Si L = K(V), on dit que L est engendré par V.
Une extension engendrée par un seul élément est appelée extension simple. Elle est finie si et seulement si elle est engendrée par un élément algébrique.
Par exemple,


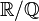
Extension radicielle
Une extension L / K est dite radicielle si tout élément x de L est une racine d'un élément de K, c'est-à-dire que
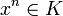
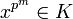
Extension séparable
Un élément algébrique d'une extension L / K est dit séparable sur K s'il annule un polynôme séparable à coefficients dans K (c'est-à-dire un polynôme premier avec son dérivé, ou de façon équivalente, un polynôme qui n'a pas de racine multiple dans une clôture algébrique de K). Une extension algébrique est dite séparable si tous ses éléments sont séparables sur K. Toute extension algébrique d'un corps parfait est séparable. Toute extension finie séparable est simple (la réciproque est cependant manifestement fausse).
Toute extension finie est extension radicielle d'une extension séparable.
Extension de Galois
Une extension finie L / K est dite de Galois ou galoisienne si elle est normale et séparable. Le groupe des automorphismes de l'extension est fini, d'ordre le degré de l'extension [L:K]. Ce groupe est appelé groupe de Galois de l'extension.
Par exemple,