Diophantien - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
L'adjectif diophantien (du nom de Diophante d'Alexandrie) s'applique à tout ce qui concerne les équations polynomiales à coefficients entiers, également appelées équations diophantiennes. Les notions qui suivent ont été développées pour venir à bout du dixième problème de Hilbert. Il s'agit de savoir s'il existe un algorithme général permettant de dire si, oui ou non, il existe une solution à une équation diophantienne. Le théorème de Matiyasevich prouve l'impossibilité de l'existence d'un tel algorithme.
Ensemble diophantien
Un ensemble M inclus dans
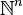
-
- a ∈ M ⇔ il existe x tel que D(a, x) = 0
Ci-dessus, D est un polynôme à coefficients entiers de n+p variables, et x est un paramètre élément de
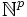
Exemple
- L'ensemble des nombres pairs est diophantien car :
-
- a pair ⇔ il existe x tel que a – 2x = 0
- L'ensemble des nombres non premiers est diophantien car :
-
- a est non premier ⇔ il existe (x,y) tel que a - (x+2)(y+2) = 0
Si M est un ensemble diophantien, inclus dans

-
- a ∈ M ⇔ il existe x, D(a, x) = 0 ⇔ il existe x dans
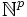

- a ∈ M ⇔ il existe x, D(a, x) = 0 ⇔ il existe x dans
donc M est l'ensemble des valeurs positives d'un polynôme à coefficients entiers, pour des valeurs positives des variables. Par exemple, l'ensemble des nombres de Fibonacci est constitué des valeurs positives du polynôme y(2 – (x2 + xy – y2)2).
Réunion et intersection d'ensembles diophantiens
On montre aisément que la réunion ou l'intersection de deux ensembles diophantiens est diophantien. En effet, si M1 et M2 sont diophantiens, représentés respectivement par les équations D1 et D2, alors :
-
- a ∈ M1 ∪ M2 ⇔ il existe (x,y) tel que D1(a,x)D2(a,y) = 0.
M1 ∪ M2 est donc diophantien, représenté par D(a,x,y) = D1(a,x)D2(a,y).
De même, M1 ∩ M2 est diophantien, représenté par D(a,x,y) = D1(a,x)2 + D2(a,y)2.
Par contre, le complémentaire d'un ensemble diophantien n'est pas toujours diophantien.
Fonction diophantienne
Une fonction F de


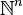
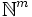
-
- a = F(b) ⇔ il existe x, D(a, b, x) = 0
Les applications polynomiales sont évidemment diophantiennes. Mais on montre également que l'exponentielle est diophantienne, autrement dit, il existe un polynôme D tel que :
-
- a = bn ⇔ il existe x, D(a, b, n, x) = 0
Nous soulignons bien que l'expression de gauche a = bn possède les trois variables a, b et n et est donc une relation exponentielle, et non une simple relation polynomiale telle que a = b3, où n s'est vu fixer la valeur 3. Il est absolument remarquable qu'une expression exponentielle puisse être caractérisée uniquement par des relations polynomiales. Cette propriété, démontrée par Matiyasevich, est un point clé de la réponse négative apportée au 10ème problème de Hilbert. On peut utiliser pour cela le fait que des suites de solutions d'équations diophantiennes peuvent croître exponentiellement. Ainsi, bn est quasiment égal à an où (an) est la suite définie par :
-
- a0 = 0, a1 = 1, an+2 = ban+1 – an
et que :
-
- il existe n, x = an et y = an+1 ⇔ x2 – bxy + y2 = 1
Ou bien, en utilisant un codage passant par l'intermédiaire de solutions d'équations de Pell-Fermat, on montre qu'il y a équivalence entre a = bn et :
-
- il existe (f,g,h,k,l,m,s,t,u,v,w,x,y,z) entiers strictement positifs tels que :
- m2 – (w2 – 1)(w – 1)2z2 = 1
- w = b + h = n + l
- a + g = 2mb – b2 – 1
- (x – y(m – b) – a)2 = (f – 1)2(2mb – b2 – 1)2
- x2 – (m2 – 1)y2 = 1
- u2 – (m2 – 1)v2 = 1
- s2 – (k2 – 1)t2 = 1
- v = ry2
- k = 1 + 4py = m + qu
- s = x + cu
- t = n + 4(d – 1)y
- y = n + e – 1
- il existe (f,g,h,k,l,m,s,t,u,v,w,x,y,z) entiers strictement positifs tels que :
On montre que les coefficients binomiaux sont diophantiens en les considérant comme coefficients dans une base b assez grande de (b+1)n. Il en est de même des factorielles et des nombres premiers.

















































