Diophantien - Définition

Propriété diophantienne

Une propriété P est diophantienne, représentée par l'équation diophantienne D si :

P(a) ⇔ il existe x tel que D(a,x) = 0

Il est équivalent de dire que l'ensemble des a vérifiant la propriété P est un ensemble diophantien. La conjonction ou la disjonction de propriétés diophantiennes est diophantienne. Par contre, la négation ou l'implication ne conserve pas le caractère diophantien.

On définit de proche en proche des propriétés diophantiennes de plus en plus compliquées, par exemple, le fait qu'un entier soit un nombre premier.

Le dixième problème de Hilbert

Le dixième problème de Hilbert consiste à définir un algorithme acceptant comme paramètre une équation diophantienne D et donnant comme réponse le fait que D admette ou non des solutions. En 1970, Matiyasevic montra qu'il était impossible qu'un tel algorithme existe.

On montre en effet qu'il y a équivalence entre les ensembles diophantiens et les ensembles reconnaissables par machine de Turing (ensembles également dits récursivement énumérables ou semi-calculables). Une machine de Turing modélise un programme donné sur un calculateur universel sans limitation de mémoire. Un ensemble récursivement énumérable E est un ensemble pour lequel il existe un algorithme tel que, si on donne comme paramètre à l'algorithme un élément a de E, alors l'algorithme s'arrête en fournissant une réponse positive, alors que si on donne comme paramètre un élément a n'appartenant pas à E, ou bien l'algorithme s'arrête en donnant une réponse négative, ou bien il boucle indéfiniment. Un ensemble récursivement énumérable est un ensemble dont on peut lister un à un les éléments. On peut être dans l'impossibilité de lister les éléments de son complémentaire.

Tout ensemble diophantien est récursivement énumérable

Il est facile de montrer qu'un ensemble diophantien E défini par une équation D est récursivement énumérable. L'algorithme le reconnaissant est le suivant :

• lire en entrée la valeur du paramètre a
• donner à x la valeur 0
• tant que D(a,x) est différent de 0, augmenter x de 1 fin tant que

Cet algorithme est donné dans le cas où x décrit . Si x doit décrire , il convient de remplacer l'énumération des éléments de par une énumération des éléments de .

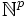
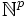
Si a est élément de E, il existera un x tel que D(a,x) = 0. L'algorithme précédent finira par le trouver et s'arrêtera sur cette valeur de x. Par contre, si a n'est pas élément de E, aucun x ne convient, et l'algorithme bouclera indéfiniment. E est donc bien récursivement énumérable.

Tout ensemble récursivement énumérable est diophantien

La réciproque est extrêmement délicate et constitue le nœud du théorème de Matiyasevich. Elle se prouve en codant les configurations d'une machine de Turing par des entiers et en montrant que la fonction qui, à une configuration de la machine au cours du calcul, associe la configuration suivante, est une fonction diophantienne. Si p est un nombre codant une configuration d'une machine de Turing, il existe un polynôme D tel que D(p, x₁, ..., x_n) possède une solution si et seulement si la Machine de Turing démarrant par la configuration p s'arrête. La reconnaissance des ensembles diophantiens est donc équivalent à celle des ensembles récursivement énumérables.

La méthode précédente permet explicitement d'associer un polynôme à un algorithme définissant un ensemble récursivement énumérable. Ainsi, en 1976, Jones a-t-il explicité un polynôme de degré 25 et des 26 variables a, b, ..., z, dont l'ensemble des valeurs positives coïncide avec l'ensemble des nombres premiers. Le voici :

(k+2)[1 – (wz+h+j–q)² – [(gk+2g+k+1)(h+j) + h – z]²

– (2n+p+q+z–e)² – [16(k+1)³(k+2)(n+1)² + 1 – f²]²

– [e³(e+2)(a+1)² + 1 – o²]² – [(a²–1)y² + 1 – x²]²

– [16r²y⁴(a²–1) + 1 – u²]²

– [((a+u²(u²–a))²–1)(n+4dy)² + 1 – (x+cu)²]² – [n+l+v–y]²

– [(a²–1)l² + 1 – m²]² – [ai+k+1–l–i]²

– [p + l(a–n–1) + b(2an+2a–n²–2n–2) – m]²

– [q+ y(a–p–1) + s(2ap + 2a – p² – 2p – 2) – x]²

– [z + pl(a–p) + t(2ap – p² – 1) – pm]²]

Impossibilité du dixième problème de Hilbert

La théorie de la calculabilité a montré qu'il existe des ensembles récursivement énumérables dont le complémentaire n'est pas récursivement énumérable.

Plus précisément, à toute équation diophantienne D sans paramètre, définissons Card(D) comme étant le cardinal de son ensemble de solutions (éventuellement infini). Alors l'ensemble E = {D | Card(D) ≥ 1} est récursivement énumérable. Car si D appartient à un tel ensemble, il suffit d'énumérer les x les uns après les autres et de tester si D(x) est nul pour finir par un trouver un, ce qui permet de dire que D appartient à E. Si D n'admet pas de solution, l'algorithme précédent boucle indéfiniment. Et précisément, on montre que {D | Card(D) = 0} n'est pas récursivement énumérable. Cela signifie qu'il existe bien un algorithme général permettant de dire si une équation diophantienne D admet une solution, mais aucun algorithme permettant de dire si D n'en admet pas.

Le dixième problème de Hilbert n'admet donc pas de solution. La résolution générale des équations diophantiennes est un problème indécidable.