Échantillonnage préférentiel - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
L'échantillonnage préférentiel, en anglais importance sampling, est une méthode de réduction de la variance qui peut être utilisée dans la méthode de Monte-Carlo. L'idée sous-jacente à l'échantillonnage préférentiel, EP dans la suite, est que certaines valeurs prises par une variable aléatoire dans une simulation ont plus d'effet que d'autres sur l'estimateur recherché. Si ces valeurs importantes se réalisent plus souvent, la variance de notre estimateur peut être réduite.
Par conséquent la méthode de l'EP est de choisir une distribution qui « encourage » les valeurs importantes. L'utilisation d'une distribution biaisée conduira à un estimateur biaisé si nous l'appliquons directement aux simulations. Cependant, les différentes simulations sont pondérées afin de corriger ce biais ; l'estimateur EP est alors sans biais. Le poids qui est donné à chaque simulation est le ratio de vraisemblance, qui est la densité de Radon-Nikodym de la vraie distribution par rapport à la distribution biaisée.
Le point fondamental dans l'implémentation d'une simulation utilisant l'EP est le choix de la distribution biaisée. Choisir ou créer une bonne distribution biaisée est l'art des EP. L'avantage peut alors être une énorme économie de temps de calculs alors que l'inconvénient pour une mauvaise distribution peut être des calculs plus longs qu'une simple simulation de Monte-Carlo.
Théorie
En Monte-Carlo
On souhaite estimer une quantité G, qui s'exprime sous la forme d'une intégrale :
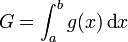
On considère ici une intégration en dimension 1, mais on peut généraliser à une dimension quelconque.
Le principe de base des méthodes de Monte-Carlo est de voir l'intégrale précédente comme
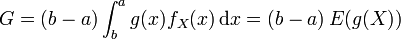
où X est une variable aléatoire uniformément distribuée sur [a;b] et
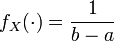
Si on dispose d'un échantillon
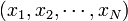
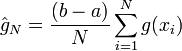
Il s'agit, d'après la loi des grands nombres, d'un estimateur de G non-biaisé (c'est-à-dire que
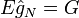
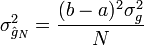
avec
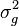
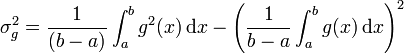
L'échantillonnage préférentiel
L'idée principale de l'échantillonnage préférentiel est de remplacer dans la simulation la densité uniforme sur [a;b] par une densité alternative (ou densité biaisée), disons
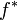
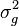
L'intégrale à estimer est ré-écrite comme:
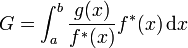
ce qui revient à:
![G = E^{\ast} [w(X)]](https://static.techno-science.net/illustration/Definitions/autres/6/672811cef2592d2bdba7cf45acfe6805_d33fc1982d0f600f9ac6c1831dea9003.png)
où on a posé
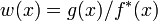
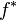
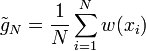
où
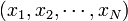
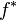
![\mbox{Var}^{\ast} (\tilde{g}_N) = \frac{\mbox{Var}^{\ast}[w(X)]}{N}](https://static.techno-science.net/illustration/Definitions/autres/f/f2f05f85e86d5ffddaf638a5c6a04f0b_a6b1efa4533ec4b3ea7a2b89b109708b.png)
avec enfin
![\mbox{Var}^{\ast}[w(X)] = \mbox{Var}^{\ast}\left[\frac{g(X)}{f^{\ast}(X)}\right]=\int_a^b \left[\frac{g(x)}{f^{\ast}(x)}\right]^2 f^{\ast}(x) \,\mbox{d}x - G^2](https://static.techno-science.net/illustration/Definitions/autres/f/f6876319e8922f5e312f7393a753e09e_aa8feeaddb132e7ac7d70413b4331314.png)
Dès lors, le problème est de se concentrer sur l'obtention d'une densité biaisée
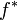
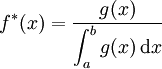
mais ce choix est inopérant, car on recherche justement le dénominateur. Mais, on peut s'attendre à réduire la variance en choisissant une densité
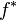
En quasi Monte Carlo
Pour estimer l'intégrale
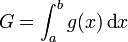
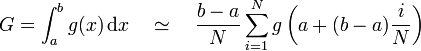
De même qu'en Monte Carlo usuel, cette approximation de l'intégrale converge d'autant plus vite que la fonction g est proche d'une constante. Si g est rigoureusement constante il suffit de prendre N = 1 pour avoir l'intégrale exacte. Réduire la variance de g est par conséquent crucial ici aussi ; dans ce but, l'échantillonnage préférentiel s'utilise comme suit :
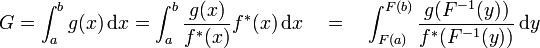
où l'on a fait le changement de variable y = F(x) avec  . Il apparaît clairement que si
. Il apparaît clairement que si
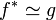
Pour faire le lien avec l'interprétation probabiliste de la section précédente, on remarque que f* est définie à un facteur K près qui disparaît dans le quotient. On peut donc imposer que
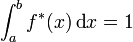
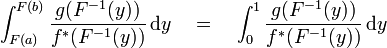
Cette technique se généralise immédiatement en dimension quelconque.