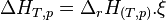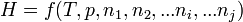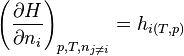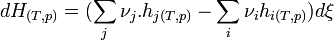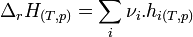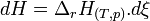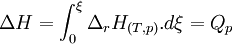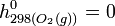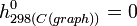Enthalpie de réaction - Définition

Introduction

L'enthalpie de réaction est une grandeur de réaction associée à l'écriture de l'équation-bilan d'une réaction chimique effectuée à température T et pression p constantes. Connaissant l'avancement de réaction, , elle permet le calcul de la variation d'enthalpie du système réactionnel.

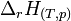
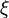
L'enthalpie de réaction s'exprime en joule par mole ( ).

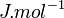
Comme la plupart des réactions chimiques ont lieu à pression constante, l'enthalpie de réaction permet d'avoir accès à la quantité d'énergie libérée sous forme de chaleur car (voir enthalpie).

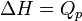
Son utilité est donc grande en génie chimique.

Une réaction chimique qui a une enthalpie de réaction négative est dite exothermique, puisqu'elle libère de la chaleur dans l'environnement, alors qu'une réaction chimique dont l'enthalpie de réaction est positive est dite endothermique: elle nécessite un apport de chaleur pour se produire.

Définition thermodynamique

Considérons une réaction chimique dont l'équation bilan est la suivante:

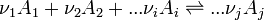
L'enthalpie du système réactionnel H est fonction des variables indépendantes T, p, n₁, n₂,... n_i, ...n_j.

La fonction enthalpie étant une fonction d'état, sa différentielle totale est exacte et peut s'écrire:

.

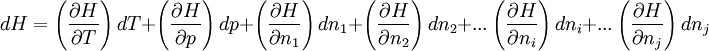
Si la réaction a lieu à température T et à pression p constantes:

.

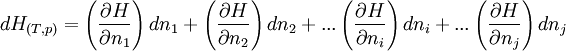
La dérivée partielle de H par rapport à chaque n, toutes les autres variables étant constantes, correspond à l'enthalpie molaire partielle du constituant considéré.

Chaque variation du nombre de mole dn est reliée à la variation de l'état d'avancement dξ.

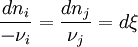
On remplace chaque dn par son expression en fonction de dξ. Puis on regroupe les termes correspondant aux réactifs i et aux produits j.

On obtient:

L'expression:

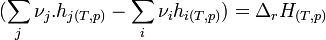
correspond à l'enthalpie de réaction de la réaction chimique envisagée à T et p constants.

L'enthalpie de réaction correspond donc à la différence des enthalpies molaires partielles entre les produits et les réactifs, en tenant compte de la stoechiométrie de la réaction.

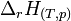
On exprime souvent cette relation sans distinguer les réactifs et les produits. Dans ce cas les coefficients stœchiométriques des produits sont positifs, alors que ceux des réactifs sont négatifs.

Calculons alors la variation d'enthalpie du système réactionnel

Intégrons pour un état d'avancement variant de zéro à ξ.

Remarque

• Pour les systèmes réactionnels idéaux ( gaz considérés comme parfaits, solutions diluées ), l'enthalpie de réaction reste constante au cours d'une réaction. La variation d'enthalpie du système réactionnel ΔH qui est égale à la chaleur Q_p, mise en jeu à pression constante, devient égale au produit de l'enthalpie de réaction par l'état d'avancement ξ:

.

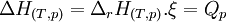
Si la réaction est totale, ξ = 1 mol.

.

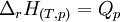
La connaissance de l'enthalpie de réaction permet donc d'avoir accès à la chaleur de réaction.

Problématique de l'état de référence

Fig. 1: L'enthalpie de réaction correspond à la différence d'enthalpie entre les produits de la réaction (à droite) et les réactifs (à gauche). Pour calculer cette différence, il est capital de disposer d'une référence commune.

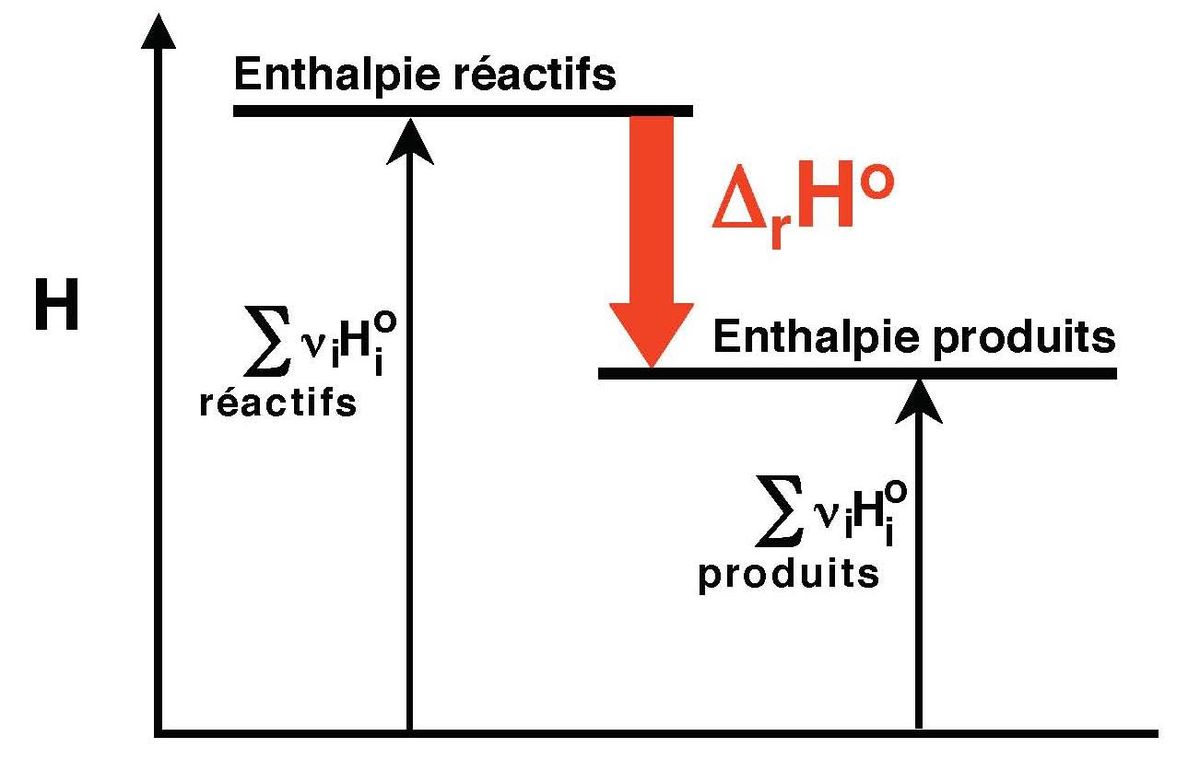
L'enthalpie molaire standard est tabulée pour de nombreux composés. Il est ainsi aisé de calculer par différence l'enthalpie de réaction, à condition de faire attention aux états de référence utilisés (Figure 1). Comme il n'existe pas de zéro absolu pour l'enthalpie, plusieurs états de références ont été définis pour les enthalpies molaires des composés.

Par analogie avec l'altitude, lorsque l'on doit calculer une dénivelée entre deux points, on calcule la différence entre leur altitudes. De manière implicite, on utilise le même état de référence, à savoir que l'altitude au niveau de la mer vaut zéro. On peut tout aussi bien utiliser un autre état de référence (par exemple en admettant que l'altitude au fond de la Fosse des Mariannes vaut zéro), mais un résultat correct n'est obtenu qu'en restant cohérent, à savoir en utilisant le même référentiel pour les points de départ et d'arrivée.

Pour dresser des tables d'enthalpies molaires standards on a choisi de définir l'échelle d'enthalpie de la manière suivante: l'enthalpie molaire standard d'un corps pur simple stable dans l'état standard est nulle à 298 K.

Exemples:

Néanmoins l'utilisation des enthalpies standards de formation permet d'éviter l'emploi d'une convention arbitraire.