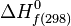Enthalpie standard de formation - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
L'enthalpie d'un corps pur ne peut être calculée de façon absolue car elle dépend de l'énergie interne qui n'est pas calculable (H = U + pV). Néanmoins, des tables d'enthalpies molaires standards ont été établies afin de pouvoir calculer rapidement une enthalpie standard de réaction à partir des valeurs de ces enthalpies molaires :
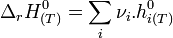
C'est pour éviter cet inconvénient qu'a été définie l'enthalpie standard de formation à T :
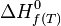
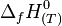
Définition
L'enthalpie standard de formation à T, d'un composé chimique,
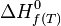
Elle correspond à l'enthalpie standard de réaction à T,
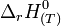
exemple : l'enthalpie standard de formation à T, de
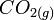
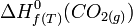
C'est l'enthalpie standard de réaction,
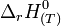
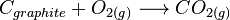
De cette définition découlent plusieurs conséquences :
- L'enthalpie standard de formation à T, d'un corps simple stable est nulle, puisque la réaction de formation c'est la réaction de formation à partir de lui-même.
-
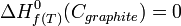
-
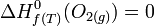
-

- Il n'est plus nécessaire de définir une échelle arbitraire d'enthalpie. On a choisi de dresser des tables d'enthalpies standards de formation à la température de référence de 298 K.
Loi de Hess
L'intérêt de l'enthalpie standard de formation est qu'elle permet de calculer le
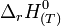
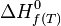
Considérons une réaction chimique dont l'équation bilan est la suivante :
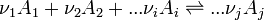
- réactifs ( i )....................................produits ( j )
L'enthalpie standard de réaction à T est égale à :
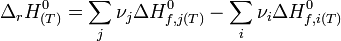
Remarque
- Ces relations sont souvent exprimées par les expressions suivantes, simplifiées mais moins explicites.
-
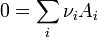
-
-
-
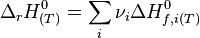
- Les produits ne sont plus distingués des réactifs et les coefficients stoechiométriques sont notés algébriquement : positifs pour les produits, négatifs pour les réactifs.
-
Grandeurs thermodynamiques de quelques composés à 298 K
Les enthalpies standards de formation et entropie standard à 298 K, sont tirées des tables publiées par la JANAF ainsi que Ribaud et Manson (Ministère de l'Air - 1961). Attention, en toute rigueur, ces enthalpies de formation ne sont plus standard car elles ne sont pas données à P = 1 bar = 105 Pa, mais à P = 1 atm = 1,01325×105 Pa, ce qui constituait la pression standard à cette date. Néanmoins, étant donnée la variation minime de pression, les valeurs reportées dans ce tableau sont proches des valeurs réelles en première approximation.
Voir État standard.
| composé chimique | Masse molaire (g) |
| S°298 (J/(mol.K)) |
| CO2(g) | 44,010 | -393,5 | 213,75 |
| CO(g) | 28,011 | -110,58 | 197,6 |
| NO(g) | 30,008 | 90,32 | 210,7 |
| NH3(g) | 17,031 | -45,91 | 192,66 |
| CH4(g) | 16,043 | -74,9 | 186,17 |
| C2H6(g) | 30,068 | -84,7 | 229,57 |
| C3H8(g) | 44,094 | -103,88 | 270,01 |
| C4H10(g) | 58,12 | -124,78 | 310,15 |
| C5H12(g) | 72,146 | -146,50 | 349,49 |
| C6H14(g) | 86,172 | -167,25 | 386,95 |
| C7H16(g) | 110,198 | -187,89 | 425,41 |
| C8H18(g) | 114,224 | -208,52 | 463,84 |
| C2H4(g) | 28,054 | 52,49 | 219,30 |
| C3H6(g) | 42,078 | 20,42 | 267,03 |
| C2H2(g) | 26,038 | 226,81 | 200,92 |
| C6H6(g) | 78,108 | 82,96 | 269,30 |
| H2(g) | 2,016 | 0 | 130,46 |
| H(g) | 1,008 | 218,06 | 114,65 |
| N2(g) | 28,016 | 0 | 191,32 |
| N(g) | 14,008 | 472,96 | 153,23 |
| O(g) | 16,000 | 249,28 | 161,02 |
| O2(g) | 32,000 | 0 | 204,82 |
| O3(g) | 48,000 | 142,12 | 237,42 |
| C (graphite) | 12,011 | 0 | 5,68 |
| C (diamant) | 12,011 | 1,92 | 2,45 |
| H2O (liquide) | 18 | -285,8 | 69,96 |
| H2O (gaz) | 18 | -241,8 | 188,74 |
Remarques :
- Les corps simples dont l'enthalpie de formation standard à 298 K est nulle, correspondent à la variété stable à cette température.
- Certains composés ne sont pas stables sous la pression standard à 298 K. C'est le cas par exemple, de l'eau à l'état gaz. Néanmoins, même si son existence est formelle dans ces conditions, on a donné la valeur de son enthalpie standard de formation à 298 K, déterminée en tenant compte de l'enthalpie de vaporisation de l'eau liquide.