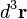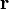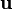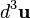Équation de Boltzmann - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Modèle mécanique du gaz - Équation de Boltzmann non-relativiste - Fonction de distribution à une particule - Limites hydrodynamiques - Équation de Boltzmann relativiste

Introduction

L'équation de Boltzmann (1872) est une équation intégro-différentielle de la théorie cinétique qui décrit l'évolution d'un gaz peu dense hors d'équilibre. Elle permet notamment de démontrer le théorème H, et d'étudier la relaxation du gaz d'un état d'équilibre local vers l'équilibre global caractérisé par la distribution de Maxwell des vitesses.

La première solution analytique complète a été obtenue dans le cas des interactions de type « sphères dures » par Ukai dans les années 1970, mais seulement pour des solutions proches de l'équilibre. La plus grande avancée reste la théorie des solutions renormalisées de Ronald DiPerna et du médaille Fields Pierre-Louis Lions qui fournit l'existence de solution, même loin de l'équilibre. Leur régularité et unicité reste un problème ouvert très important.

Modèle mécanique du gaz

On considère un gaz de sphères dures constitué de $N$ atomes identiques de masse $m$ et de rayon $r$ . Ces atomes :

sont confinés dans une boîte ;

voyagent à vitesse constante entre les collisions ;

rebondissent élastiquement les uns sur les autres ;

rebondissent élastiquement sur les parois de la boîte.

Équation de Boltzmann non-relativiste

Opérateur de Liouville non-relativiste

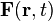
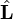
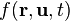
Soit un gaz placé dans un champ de force externe macroscopique $\mathbf{F}(\mathbf{r}, t)$ (par exemple, le champ de pesanteur local). L'opérateur de Liouville $\hat{\mathbf{L}}$ décrivant la variation totale de la fonction de distribution à une particule $f(\mathbf{r}, \mathbf{u}, t)$ dans l'espace des phases à une particule est l'opérateur linéaire défini en mécanique non-relativiste par :

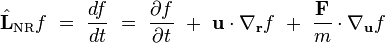
$\hat{\mathbf{L}}_\mathrm{NR}f \ = \ \frac{d f}{d t} \ = \ \frac{\partial f}{\partial t} \ + \ \mathbf{u}\cdot\nabla_\mathbf{r}f \ + \ \frac{\mathbf{F}}{m}\cdot\nabla_\mathbf{u}f$

Équation de Boltzmann non-relativiste

Du fait des collisions, la fonction de distribution à une particule possède une variation totale non-nulle ; elle obéit à l'équation de Boltzmann :

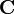
$\hat{\mathbf{L}}[f] \ = \ \mathbf{C}[f]$

où $\mathbf{C}$ est l'opérateur de collision, opérateur intégral non-linéaire. Historiquement, Boltzmann a obtenu l'expression analytique de cet opérateur de collision par une analyse fine des collisions à deux corps. Il est également possible de dériver l'équation de Boltzmann par une troncature appropriée des équations de la hiérarchie BBGKY.

Théorème de Lanford

Limite de Boltzmann-Grad

La limite dite de Boltzmann-Grad consiste à prendre la limite conjointe :

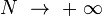
d'un nombre d'atomes $N \ \to \ + \ \infty$ ;

d'un rayon $r \ \to \ 0$ ;

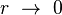
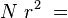
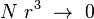
en maintenant le produit $N \ r^2 \ = \$ cte. En particulier, le volume exclu tend vers zéro dans cette limite : $N \ r^3 \ \to \ 0$

Théorème de Lanford (1973)

Lanford a démontré rigoureusement qu'un gaz de sphères dures dilué dans $\mathbb{R}^3$ obéit à l'équation de Boltzmann dans la limite de Boltzmann-Grad, au moins pour un temps très court, égal seulement à un cinquième du temps de parcours moyen d'un atome.

En dépit de cette restriction sur la durée, ce théorème mathématique rigoureux est très important conceptuellement, puisque l'équation de Boltzmann entraine le théorème H, à propos duquel Boltzmann fut accusé de pratiquer des « mathématiques douteuses ». Il n'en demeure pas moins qu'il reste à démontrer que ce résultat reste vrai pour des temps macroscopiques, ainsi que lorsque les atomes sont confinés dans une boite.

Fonction de distribution à une particule

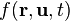
On note $f(\mathbf{r}, \mathbf{u}, t)$ la fonction de distribution à une particule du gaz, telle que :

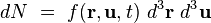
$dN \ = \ f(\mathbf{r}, \mathbf{u}, t) \ d^3 \mathbf{r} \ d^3\mathbf{u}$

représente le nombre de molécules de gaz situées à l'instant $t$ dans un petit volume d'espace $d^3\mathbf{r}$ autour du point $\mathbf{r}$ et ayant une vitesse $\mathbf{u}$ définie à $d^3\mathbf{u}$ près.