Théorème H - Définition

Introduction

Le théorème H est un théorème démontré par Boltzmann en 1872 dans le cadre de la théorie cinétique des gaz, lorsqu'un gaz hors d'équilibre vérifie son équation. Selon ce théorème, il existe une certaine grandeur H(t) qui varie de façon monotone au cours du temps, pendant que le gaz relaxe vers l'état d'équilibre caractérisé par la distribution de Maxwell.

Aspects historiques

La théorie cinétique des gaz, qui est basée sur l'application de la mécanique classique aux molécules constituant le gaz à l'échelle microscopique, s'est développée à partir des travaux fondateurs de Maxwell (1850) en parallèle avec la thermodynamique macroscopique. Boltzmann a contribué de façon marquante à la maturation de la théorie cinétique des gaz.

Il semblait tentant d'identifier la grandeur H(t), qui varie de façon monotone au cours du temps, à l'entropie (au signe près) introduite en thermodynamique par Clausius (1850) et qui, pour un système isolé, ne peut que croître d'après le second principe. Cette identification aurait permis de déduire le second principe, macroscopique, à partir des lois de la dynamique des molécules, microscopiques, conformément à l'approche réductionniste de la Nature.

Rapidement cependant, Loschmidt, puis Zermelo, formulèrent des critiques virulentes contre le théorème H, Boltzmann étant accusé de pratiquer des « mathématiques douteuses ». Cette accusation ne tient plus depuis un théorème rigoureux démontré par Lanford en 1973 (lire ci-dessous).

Le paradoxe de la réversibilité

Le paradoxe de Loschmidt (1876)

Loschmidt se demande comment la grandeur H(t) peut-elle varier de façon monotone au cours du temps alors que les équations de la mécanique classique sont réversibles ? En effet, si la fonction H(t) était en train de décroitre et qu'à un instant donné, on renverse exactement toutes les vitesses de molécules, alors la nouvelle évolution se fait à l'envers, avec H(t) commençant par croitre. La réponse de Boltzmann fut brêve : « Allez-y, renversez les !  », signifiant l'impossibilité pratique d'une telle inversion exacte.

Interprétation statistique de l'entropie (Boltzmann-1877)

En 1877, Boltzmann proposa une nouvelle définition de l'entropie :

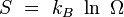
où k_B est la constante de Boltzmann, et Ω le « nombre de complexions », c’est-à-dire le nombre de micro-états différents qui sont compatibles avec le macro-état thermodynamique donné.

La croissance de l'entropie devait alors être interprétée comme un phénomène statistique : l'entropie croît parce que le système évolue en général d'un état initial improbable (Ω_i petit) vers un état final beaucoup plus probable (Ω_f > Ω_i). Des fluctuations locales sont bien sûr possibles, mais leur grandeur relative tend vers zéro lorsque le nombre N de molécules tend vers l'infini, de telle sorte que l'entropie d'un système macroscopique nous semble croître de façon monotone.

Inversion des vitesses & sensibilité aux conditions initiales

Avec la découverte du phénomène de sensibilité aux conditions initiales caractéristique des systèmes chaotiques, nous savons aujourd'hui qu'une inversion approchée des vitesses va rapidement entraîner une déviation par rapport à l'orbite initiale exacte inversée, et ce aussi petites que soient les erreurs introduites sur les conditions initiales. Des simulations numériques montrent alors qu'après une inversion approchée, la fonction H(t) commence bien par décroître comme le prédisait Loschmidt, mais qu'elle se remet très rapidement à croître à nouveau et ce pour presque toutes les conditions initiales approchées, l'orbite réelle du système différant de l'orbite initiale exacte inversée.

Le paradoxe de Zermelo

Le paradoxe de Zermelo (1896)

En 1890, alors qu'il étudie le problème à 3 corps en mécanique céleste, Poincaré démontre un théorème très général : le théorème de récurrence. Ce théorème dit que, pour presque toutes les conditions initiales, un système dynamique conservatif dont l'espace des phases est de volume fini va repasser au cours du temps aussi près que l'on veut de sa condition initiale, et ce de façon répétée.

Zermelo fait alors remarquer à Boltzmann en 1896 que le théorème de récurrence de Poincaré semble contredire le fait qu'une grandeur dynamique puisse varier de façon monotone, comme H(t) le fait. La réponse de Boltzmann consiste à estimer le temps de récurrence moyen : pour un gaz macroscopique contenant molécules, Boltzmann estime celui-ci d'ordre 10^N, une durée qui est largement supérieure à l'age de l'univers lorsque  ; les récurrences sont donc invisibles à notre échelle. (Voir illustration à Modèle_des_urnes_d'Ehrenfest#Dynamique du modèle.)

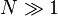
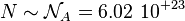
Le modèle des urnes d'Ehrenfest (1907)

Le « modèle des urnes » est un modèle stochastique introduit en 1907 par les époux Paul & Tatiana Ehrenfest pour clarifier les paradoxes précédents apparus à la fin du XIX^e siècle dans les fondements de la mécanique statistique. Ce modèle est parfois également appelé le « modèle des chiens & des puces  ». Le mathématicien Mark Kac a écrit à son propos qu'il était :

«  ... probablement l'un des modèles les plus instructifs de toute la physique ...  »

Ce modèle est exactement soluble ; en particulier, on sait calculer le temps de récurrence moyen de chaque état, ainsi que sa variance pour certains états intéressants.

Le théorème de Lanford (1973)

Lanford a démontré rigoureusement qu'un gaz de sphères dures dilué dans obéit à l'équation de Boltzmann dans la limite de Boltzmann-Grad, au moins pour un temps très court, égal seulement à un cinquième du temps de parcours moyen d'un atome.

En dépit de cette restriction sur la durée, ce théorème mathématique rigoureux est très important conceptuellement, puisque l'équation de Boltzmann entraine le théorème H. Il est donc aujourd'hui acquis que les mathématiques de Boltzmann ne sont pas « douteuses » !