Fenêtre de tir - Définition

Introduction

Une fenêtre de tir en astronautique est la période pendant laquelle les conditions optimales pour le lancement d'une fusée sont réunies.

Soit la Terre supposée sphérique. Le champ gravitationnel est donc central et en . L'orbite d'un satellite suivra les lois de Kepler. Pour mettre un satellite en orbite circulaire à la distance , il faut une vitesse initiale perpendiculaire à et de module telle que soit

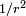
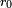
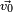
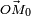
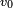
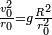
dans laquelle est la première première vitesse cosmique pour la Terre,ou vitesse de Schuler, c'est-à-dire la vitesse, toute théorique, à laquelle il faurdait lancer un satellite pour qu'il se mette en orbite au ras du sol.

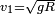
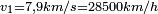
En fonction de l'altitude , définie par , la vitesse sur l'orbite circulaire s'exprime par

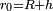
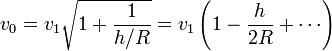
Par exemple:

• pour les satellites militaires et d'observation :
• pour Jason, Spot, les satellites héliosynchrones  :

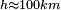
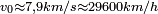
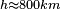
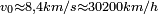
La question se pose alors de savoir ce qui se passe si on se trompe un peu sur la vitesse, en module ou en direction. En particulier de savoir s'il a risque que le satellite ne s'écrase dans l'atmosphère?

C'est le problème dit de la fenêtre de tir

Bonne direction, Mauvaise vitesse

Si le satellite est lancé dans la bonne direction mais avec une vitesse trop grande, alors le satellite est largué au périgée. Il est à la distance minimale de la terre et ne tombera plus.

Si le satellite est lancé dans la bonne direction mais avec une vitesse réelle plus petite que la vitesse nominale , le satellite est alors largué à l'apogée. Il faut que le périgée, à l'opposé de la trajectoire, soit à une distance supérieure au rayon terrestre . Autrement dit que le grand axe .

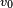
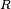
On rappèle la formule donnant l'énergie mécanique de l'orbite limite .

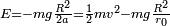
On doit donc avoir . Autrement dit, on doit avoir

.

Pour , la vitesse réelle ne doit pas être inférieure à de la vitesse nominale. Et pour , la tolérance tombe à  !

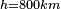
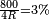
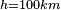
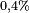
Bonne vitesse, Mauvaise direction

Bon module, donc bonne énergie donc 2a = 2r°. Donc M° est l'extrémité B du petit axe, qui se projette au centre C de l'ellipse , sur la droite parallèle à V°, passant par O : donc l'excentricité e vaut sinα : le périgée sera à OP= a-c = r°(1-sinα)

      soit sinα < h/R , donc α < (~h/R) (=1/8 rd= 7° pour Spot).      

et ~1° pour h = 100km: c'est une petite fenêtre de tir, sans gravité : on sait pointer à mieux que le demi-degré.