Forme différentielle - Définition

Opérations sur les formes différentielles

La manipulation des formes différentielles en pratique exige un ensemble d'opérations élémentaires. Certaines sont purement algébriques et se définissent en réalité pour toutes applications multilinéaires alternées. D'autres sont propres à la topologie différentielle et aux formes différentielles.

Opérations algébriques

Par définition, l'ensemble des formes différentielles (réelles) de degré k sur une variété différentielle M forme un module Ω^k(M) sur . En particulier, les formes différentielles de degré k s'additionnent ou peuvent être multipliées par des fonctions réelles :

 ;

.

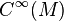
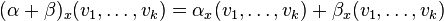
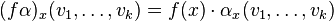
Produit intérieur 

Le produit intérieur se définit en algèbre linéaire, définition qui s'étend naturellement aux formes différentielles. Si X est un champ de vecteurs et α une forme différentiuelle de dimension k, on définit une forme différentielle de degré k − 1, par : .

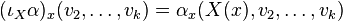
Produit extérieur 

Le produit extérieur de deux formes différentielles α et β de degrés respectifs k et q se définit comme suit : , où désigne la signature de la permutation σ et la somme porte sur toutes les permutations σ de [1,k + q] croissantes sur les k premiers entiers et croissante sur les q derniers. Le résultat est une forme de degré k + q.

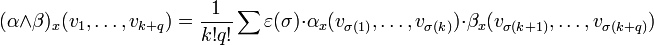
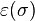
Ces opérations munissent d'une structure d'algèbre graduée commutative. Ici, commutatif signifie que pour toutes formes différentielles α et β de degrés respectifs k et q, on a :

.

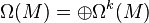
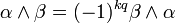
Tiré en arrière (pullback) 

Si est un difféomorphisme local, et si α est une forme différentielle de degré k sur N, on définit f ^* α comme une forme différentielle de degré k sur M par :

.

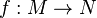
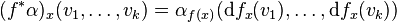
L'application définit un morphisme d'algèbre graduée.

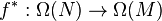
Dérivée extérieure

Dérivée de Lie

Une 0-forme différentielle est une fonction différentiable f ; considérer sa dérivée selon un champ de vecteurs X consiste à introduire la fonction df(X). La dérivée de Lie d'une forme différentielle α de degré k selon un champ de vecteurs X est une forme différentielle de degré k notée définie par :

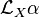
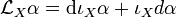
Intégration des formes

Les formes différentielles de degré k sont intégrées sur des chaînes de dimension k. Si k est nul, alors il s'agit d'une évaluation des fonctions aux points considérés. D'autres valeurs de k, avec k > 0, correspondent aux intégrales curvilignes, de surface, de volume, etc.

Soit

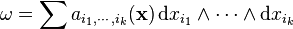
une forme différentielle et S l'ensemble d'intégration paramétrisé par :

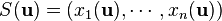
avec u un paramètre dans le domaine D. Alors [Rudin, 1976] définit l'intégrale de la forme différentielle sur S par :

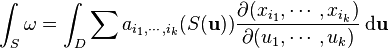
où

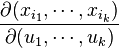
est le déterminant jacobien.