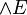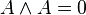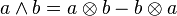Produit extérieur - Définition

En mathématiques, la notion de produit extérieur permet de rendre compte de façon algébrique des notions de parallélogrammes, parallélépipèdes, etc... de dimensions quelconques, vus comme produits des vecteurs qui en représentent les côtés.

Le contraste entre cette idée initiale fort simple, en partie accessible à un élève de grande section de maternelle ou en tout cas de l'école primaire, pour autant qu'il aura déjà aplati une boîte en carton, et la difficulté d'une présentation rigoureuse des différentes acceptions de l'expression "produit extérieur", réservée aux étudiants de licence ou de maîtrise, est remarquable.

Parmi les obstacles à la compréhension de la notion de produit extérieur, il faut insister sur le fait que la notation (dit wedge) universellement employée pour désigner le produit extérieur, opération associative pouvant porter sur les vecteurs de tout espace vectoriel, coïncide malheureusement avec celle employée en France pour désigner une opération non associative portant uniquement sur les vecteurs d'un espace euclidien orienté à trois dimension et appelée produit vectoriel. De natures différentes, ces deux opérations entretiennent des relations étroites (liées à la dualité de Hodge), d'où un risque de confusion (la situation est meilleure en anglais, le produit vectoriel, appelé "cross product", y étant le plus souvent noté ). Plus généralement, du fait de l'existence de nombreux isomorphismes plus ou moins naturels entre les objets en jeu, les domaines concernés par le calcul extérieur sont affectés d'un certain nombre de variations terminologiques et de notations selon les communautés scientifiques qui les emploient, variations qui peuvent aussi être sources de confusion.

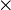
Selon le point de vue le plus classique, le fait qu'un parallélépipède appuyé sur une famille de vecteurs soit "aplati" dès que cette famille est liée conduit à envisager le produit extérieur comme résultant d'une antisymétrisation du produit tensoriel, c'est-à-dire de la forme la plus générale de produit associatif. Une telle antisymétrisation est réalisée par un passage au quotient, en l'occurrence le quotient de l'algèbre tensorielle associée à l'espace vectoriel sur lequel on travaille par l'idéal bilatère de cette algèbre qu'y engendrent les carrés tensoriels , puisque ceux-ci sont destinés à être "aplatis". On obtient ainsi l'algèbre extérieure d'un espace vectoriel E. Ainsi, d'une certaine façon, la notion d'algèbre extérieure d'un espace vectoriel précède celle du produit extérieur de deux vecteurs.

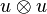
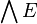
Le produit extérieur et le produit tensoriel agissant au sein d'algèbres différentes, il n'est en principe pas possible de combiner dans une même expression des produits tensoriels et des produits extérieurs. Ainsi, la formule

parfois présentée comme une définition du produit extérieur ne doit pas être prise au pied de la lettre, mais comme exprimant la possibilité d'injecter l'espace vectoriel dans , où désigne le sous-espace vectoriel de l'algèbre extérieure engendré par les "parallélogrammes" (ou bivecteurs) . Cette injection permet en effet d'identifier à un sous-espace de , en identifiant le bivecteur au tenseur antisymétrique . Laurent Schwartz dans son ouvrage "Les tenseurs" (Hermann, 1975) indique (p. 103) qu'une telle identification est peu recommandée.

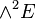
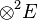
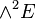
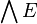
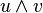
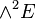
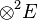
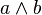
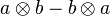
Cependant, dans le cas particulier où l'espace vectoriel E est donné comme l'espace dual F ^* d'un espace F, et s'interprètent alors naturellement comme, respectivement, algèbre des formes multilinéaires alternées et algèbre des formes multilinéaires sur F. Dans ce cas, les espaces vectoriels sont naturellement des sous-espaces des . En particulier, de ce point de vue, le produit extérieur de deux formes linéaires est la forme bilinéaire alternée définie par la formule

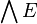
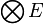
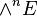
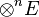
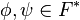
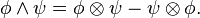
Dans l'algèbre extérieure , on n'a pas en général .