Forme différentielle - Définition

Introduction

En géométrie différentielle, une forme différentielle est la donnée d'un champ d'applications multilinéaires alternées sur les espaces tangents d'une variété différentielle possédant une certaine régularité. Le degré des formes différentielles désigne le degré des applications multilinéaires. La différentielle d'une fonction peut être regardée comme un champ de formes linéaires : c'est le premier exemple de formes différentielles. Au-delà de cet exemple, non seulement les formes différentielles interviennent naturellement dans les problèmes de géométrie différentielle, mais elles permettent de définir des structures importantes, comme les formes volumes, les formes symplectiques, les formes de contact ou encore les connexions.

La manipulation des formes différentielles fait intervenir un certain nombre d'opérations, dont le produit extérieur, le produit intérieur, la dérivée extérieure et la dérivée de Lie. En particulier, le produit extérieur permet de distinguer les formes fermées et les formes exactes. Cette distinction permet dans un second temps de définir les espaces de cohomologie de De Rham.

Les problèmes de régularité ne sont pas abordés dans cet article. On fera donc implicitement l'hypothèse que les fonctions introduites sont de classe .

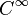
Définitions

Forme différentielle de degré un

Les formes différentielles de degré 1 – ou 1-formes – sont des champs de formes linéaires sur une variété différentielle. Dit autrement, on se donne une forme linéaire en chaque espace tangent T_xM avec une dépendance régulière en x. La dépendance en x peut facilement être précisée par l'expression dans des cartes locales. On les appelle parfois covecteurs ou champs de covecteurs ; ces outils ont des propriétés analogues aux champs de vecteurs. Il existe en réalité un isomorphisme une fois introduite par exemple une métrique riemannienne. Si f est une fonction réelle différentiable, sa différentielle df est une 1-forme différentielle (dite exacte) qui en chaque point x vaut la forme linéaire df(x). Localement, les 1-formes différentielles s'expriment comme combinaisons de différentielles de fonctions.

Plus exactement, le dual de l'espace vectoriel réel est un espace vectoriel de dimension n. Si (x₁,...,x_n) désigne les coordonnées dans , alors on note dx_i l'application i-ème coordonnée. Les formes linéaires sur s'expriment comme des combinaisons à coefficients réels des formes linéaires dx₁,...,dx_n. Les 1-formes différentielles s'expriment alors comme des combinaisons des dx₁,...,dx_n dont les coefficients dépendent de manière du point de base :

.

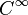
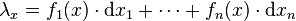
Sur une variété différentielle M, une 1-forme différentielle s'exprime localement comme ci-dessus dans les cartes locales. L'exemple le plus simple est la différentielle d'une fonction en un point a

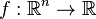
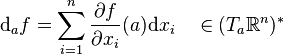
Si X est un champ de vecteurs sur M et λ est une 1-forme différentielle, alors est différentiable ; cette fonction est linéaire en X. Cela permet de regarder une 1-forme différentielle comme une forme linéaire sur le module des champs de vecteurs sur M (dont l'anneau de base est les fonctions de M dans ).

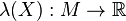
Définition comme champ de formes multilinéaires alternées

Les formes différentielles se définissent comme une extension en géométrie différentielle des formes multilinéaires alternées.

Pour une variété différentielle M, une forme différentielle ω de degré k sur M est un champ d'applications k-linéaires alternées sur les espaces tangents T_xM avec une dépendance régulière en x : pour tous champs de vecteurs X₁,...,X_k, la fonction est de classe .

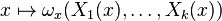
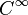
De même que pour les 1-formes différentielles, il est possible de donner l'expression locale des formes différentielles de degré k grâce au produit extérieur (voir plus bas).

Définition comme section d'un fibré

L'ensemble des applications multilinéaires alternées sur T_xM forme un espace vectoriel noté . L'ensemble de ces espaces forme ce qu'on appelle un fibré vectoriel sur M, noté ΛT ^* M, formellement la k-ième puissance du fibré cotangent de M. Une forme différentielle de degré k peut se redéfinir comme une section globale de ce fibré vectoriel.

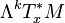
Cette approche permet non seulement de donner une meilleure signification à la régularité de la forme différentielle, mais permet aussi d'étendre la définition des formes différentielles. Si E est un fibré vectoriel sur M, une forme différentielle de degré k à valeurs de E est une section globale du produit tensoriel . C'est donc un champ d'applications muiltilinéaires alternées à valeurs dans les fibres de E. De telles formes peuvent aussi être définies comme des applications multilinéaires alternées du module X(M) dans le module des sections globales de E.