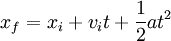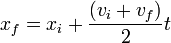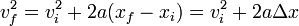Formules de physique - Définition

Introduction

La physique est une science dont une des expressions les plus précises et utiles pour faire des prévisions est le langage mathématique. Des lois physiques traduisent les phénomènes et observation, et souvent leur expression mathématique est courte et explicite ... pour ceux qui maîtrisent cet outil que sont les mathématiques.

Les formules de physique sont des expressions qui montrent les relations entre la matière, l'énergie, le mouvement, et les forces dans ce langage mathématique. La vision des formules multiples sur une page peut permettre de comprendre les relations entre les variables, après un cours de physique de base de niveau secondaire (typiquement proposé aux 16-18 ans).

L'objectif de cette page est de présenter les relations (formules) principales sous forme mathématique autant que verbale, pour que les élèves en aient une meilleure compréhension. La formulation verbale de nombreuses relations doit encore être ajoutée ou précisée.

Signification des symboles

 : accélération

 : surface ou amplitude

 : vitesse de la lumière

 : énergie

 : force

 : force résultante

 : force de frottement cinétique

 : force de frottement statique

 : accélération de la gravité

 : percussion mécanique

 : énergie cinétique

 : masse

 : coefficient frottement cinétique

 : coefficient de frottement statique

 : force normale à une surface ou un axe

 : fréquence

 : vitesse angulaire

 : quantité de mouvement

 : puissance

 : quantité de chaleur

 : rayon

 : distance parcourue

 : période

 : temps

 : angle (voir les annotations à côté de chaque formules)

 : énergie potentielle

 : volume

 : volume de fluide déplacé

 : vitesse finale

 : vitesse initiale

 : position finale

 : position initiale

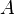
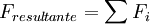
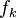
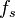
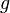
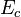
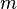
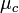
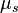
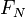
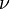
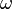
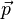
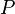
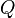
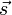
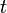
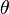
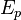
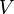
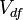
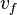
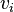
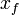
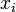
Dynamique

Comme la cinématique, la dynamique concerné le mouvement mais cette fois en prenant en compte la force et la masse des objets.

 : une force agissant sur un mobile communique à celui-ci une accélération inversément proportionnelle à sa masse. C'est la seconde loi de Newton

( est l'angle entre la surface de support et la verticale) : la force normale (perpendiculaire) exercée par une surface faisant un angle avec l'horizontale, sur un corps est la projection de son poids sur cette direction perpendiculaire

 : la force de frottement cinétique, qui apparaît lorsque le point de contact entre l'object est en mouvement l'une par rapport au support, est proportionnelle à la force avec laquelle le support agit sur l'objet.

 : la force de frottement statique, qui apparaît lorsque le point de contact entre l'object est immobile l'une par rapport au support, est proportionnelle à la force avec laquelle le support agit sur l'objet. Cette dernière est presque toujours plus grande que la force de frottement cinétique (donc μ_s > μ_c)

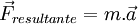
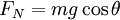
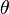
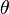
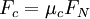
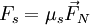
Cinématique du MRUA ou des cas où l'accélération est constante

Les formules de cinématique lient la position d'un objet, sa vitesse, et son accélération, sans tenir compte de sa masse et des forces qui s'exercent sur lui.

 : la vitesse d'un mobile en un instant est la dérivée de la position x(t) en fonction du temps, c'est-à-dire aussi la pente de la tangente à la courbe x(t) de la position en fonction du temps en cet instant.

 : l'accélération d'un mobile en un instant est la dérivée de la vitesse v(t) en fonction du temps, c'est-à-dire aussi la pente de la tangente à la courbe v(t) de la vitesse en fonction du temps en cet instant.

 : la vitesse varie linéairement avec le temps

 : l'espace parcouru (ou la position) varie quadratiquement (comme une parabole) avec le temps

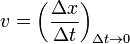
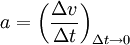
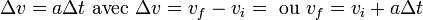
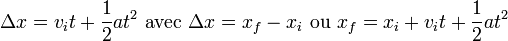
d'où l'on peut déduire aussi les relations