Groupe alterné - Définition
La liste des auteurs de cet article est disponible ici.
Classes de conjugaison
Structure
La structure des classes de conjugaison est l'un des premiers éléments à étudier dans le cadre d'une analyse d'un groupe non abélien. Elles sont utilisées dans la suite de l'article pour établir que si n est strictement supérieur à 4, le groupe est simple, ou encore que tout groupe simple d'ordre 60 est isomorphe à A5.
Dans un groupe symétrique, les classes de conjugaison sont composées de produits de cycles à supports disjoints de même structure, c'est-à-dire de même nombre et de même longueur. En conséquence, les classes de conjugaison du groupe alterné sont aussi composées de produits de cycles à supports disjoints de même structure, plus précisément :
-
- Une classe de conjugaison est constitué d'éléments ayant la même structure. Si la structure est composée uniquement de cycles de longueurs impaires, où les cycles de longueur 1 sont comptés, sans cycle de même longueur, alors il existe exactement deux classes de conjugaison. Il n'en existe qu'une sinon.
Une classe de conjugaison, ou deux dans les cas de A3 et A4, joue un rôle particulier, celle constituée des cycles d'ordre 3 :
-
- Les cycles d'ordre 3 engendrent le groupe alterné.
Établir la nature des classes de conjugaison de An est simplifié par le travail équivalent pour le groupe symétrique. Si φ1 et φ2, désignent deux permutations ayant même structure, la démonstration pour le groupe symétrique montre l'existence d'une permutation σ tel que σ-1φ1σ = φ2. On suppose ici que φ1 et φ2 sont des permutations paires. L'objectif est d'établir quand σ peut être choisi pair et ce qui se passe sinon.
-
- Une classe de conjugaison est constituée d'éléments ayant la même structure. Si la structure est composée uniquement de cycles de longueurs impaires, sans cycle de même longueur, il existe exactement deux classes de conjugaison. Il n'en existe qu'une sinon :
Commençons par établir le cas où il n'existe qu'une classe de conjugaison par structure :
- S'il existe deux entiers distincts invariants par φ2, σ peut être choisi pair. En effet, soit a et b les deux entiers invariant par φ2 et τ la transposition permutant a et b. La transposition τ commute avec φ2, ce qui montre que (σ τ)-1φ1(σ τ) = φ2. Soit σ τ soit σ est pair, ce qui établit la proposition dans ce cas là.
- S'il existe un cycle d'ordre pair dans la décomposition de φ2 en cycles à supports disjoints, σ peut être choisi pair. Ici τ désigne le cycle de φ2 ayant un ordre pair. Une fois encore τ est une permutation impair qui commute avec φ2. Le même raisonnement que précédemment montre que soit σ τ soit σ est pair et permet de conclure.
- S'il existe deux cycles de même longueur et de longueurs différentes de 1, σ peut être choisi pair. Deux cas se présentent, les cycles sont soit pairs soit impairs. S'ils sont pairs, la démonstration précédente permet de conclure. S'ils sont impaires, soient (a1a2...ak) et (b1b2...bk) ces deux cycles. Ici k désigne un entier impair. On définit τ comme égal au produit des k transpositions (a1b1)(a2b2)...(akbk). La permutation τ revient à intervertir les aj avec les bj, elle commute avec φ2. Comme k est un entier impair, la permutation τ est impaire. Le raisonnement précédent permet de conclure.
Établissons le cas où la classe de conjugaison de Sn est divisé en deux :
- Il existe au plus 2 classes de conjugaison pour une structure de cycle donnée. Soit (b1b2...bk) le premier cycle d'ordre différent de 1 de φ2. Soit τ la transposition permutant bk-1 et bk On remarque que φ3 le conjugué de φ2 par τ possède exactement les mêmes cycles que φ2, sauf celui étudié, qui devient (b1b2...bkbk-1). Ainsi, une permutation φ1 de même structure que φ2 est, soit conjuguée à φ2, soit à φ3. Il ne peut donc exister plus de 2 classes de conjugaison.
Le raisonnement pour établir le résultat pour les cycles d'ordre n, si n est impair, est un cas particulier plus simple à comprendre que le cas général. Le lecteur averti peut sauter cette partie de la démonstration.
- Si n est impair strictement supérieur à 1, il existe exactement deux classes de conjugaison contenant des cycles d'ordre n. Pour démontrer cette propriété, il suffit de montrer que (12...n-1n) n'est pas conjugué avec (12...nn-1). Les résultats précédents montrent l'existence d'une permutation impaire, à savoir la transposition σ (n-1 n), tel que le conjugué de (12...n-1n) par σ est égal à (12...nn-1). Si les deux permutations (12...n-1n) et (12...nn-1) sont conjuguées dans le groupe alterné, il existe une permutation τ de signature impaire tel que conjugué de (12...n-1n) par σ τ est égal à (12...nn-1), ce qui revient à dire que τ commute avec (12...nn-1). Autrement dit, si le centralisateur d'un cycle d'ordre n contient une permutation impaire, il n'existe qu'une classe de conjugaison, dans le cas contraire il en existe 2. Démontrer cette propriété revient à montrer que le centralisateur ne contient que des permutations paires. Calculons, dans le groupe symétrique d'indice n, le cardinal de la classe d'un cycle d'ordre n. Tout élément de la classe s'écrit (1ψ(2)ψ(3)...ψ(n)) où ψ désigne une permutation de l'ensemble des entiers compris entre 2 et n. Il existe (n - 1)! permutations de cette nature. L'ordre du centralisateur du cycle que multiplie le cardinal de sa classe est égal à l'ordre du groupe symétrique , ce résultat est connu sous le nom de formule de Burnside (cf Action par conjugaison). On en déduit que l'ordre du centralisateur est égal à n. Les n premières puissances du cycle sont des éléments distincts du centralisateur, le centralisateur est le groupe cyclique composé des puissances du cycle car il contient exactement n éléments. Ce groupe cyclique est composé de produits de permutations paires et ne contient que des permutations paires. Il ne peut donc exister de permutation τ de signature impaire dans le centralisateur du cycle, ce qui établit la propriété.
Le raisonnement du cas général est de même nature que le cas précédent :
- Si la structure n'est pas celle de l'un des cas où il est établi qu'il existe une unique classe de conjugaison, alors il en existe deux. En effet, soit φ une permutation de An qui ne correspond pas à l'un des cas où il est établi que qu'il existe une unique classe de conjugaison. Démontrer cette propriété revient à montrer que le centralisateur Gφ de φ, dans Sn ne contient que des permutations paires. Soient γ1, γ2, ..., γp les cycles à supports disjoints dont le produit est égal à φ et n1, n2, ..., np l'ordre des différents cycles. On suppose de plus que la suite des nj est strictement décroissante. Comme on compte aussi les cycles d'ordre 1, la somme des nj, où j varie de 1 à p, est égale à n. Le sous groupe de Sn engendré par les différents cycles γj est inclus dans Gφ. L'objectif est de montrer que ce groupe est exactement égal à Gφ. C'est un groupe abélien d'ordre le produit des nj pour j variant de 1 à p. Il suffit de montrer que le cardinal Cφ de la classe de conjugaison de φ est égal à n! que divise le produit des nj. Le fait que l'ordre de Gφ que multiplie Cφ soit égal à l'ordre de Sn, c'est-à-dire n! permet de conclure. Calculons dans un premier temps Np, le nombre de manières possibles de partitionner un ensemble de n éléments en p sous-ensembles tel que le jième contienne nj élément. On raisonne par récurrence. On peut supposer p supérieur ou égal à 2 car le cas où p est égal à 1 est traité dans le paragraphe précédent. On veut montrer que :
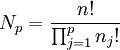
- Si p est égal à 2, comme n1 ne peut être égal à n2, la formule est vérifiée et correspond à celle du coefficient binomial. Dans le cas général, on trouve que Np est égal à Np-1 que multiplie le nombre de manières de partitionner un ensemble de n éléments en deux parties dont l'une contient np éléments. Comme la somme des n - np est différente de np, l'hypothèse de récurrence montre que :
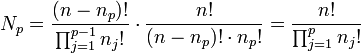
- Il a été établi qu'il existe exactement (nj - 1)! cycles d'ordre nj, ce qui montre que :
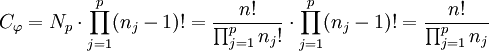
- Le fait que l'ordre de Gφ que multiplie Cφ soit égal à n! montre que l'ordre de Gφ est bien égal au produit des nj, ce qui est exactement l'ordre du groupe engendré par les cycles γi. Le deuxième groupe est inclus dans le premier et leurs ordres sont égaux. On en conclut qu'ils sont égaux. Chaque cycle est de signature paire car l'ordre des cycles est impair. Le produit de permutations de signatures paires est de signature paire, Gφ ne contient que des permutations de signature paire. Un raisonnement analogue à celui du cas du cycle d'ordre n permet de conclure.
La démonstration du fait que les cycles d'ordre 3 engendrent le groupe alterné est comparable à un jeu de taquin.
-
-
- Les cycles d'ordre 3 engendrent le groupe alterné.
-
- Soit φ une permutation du groupe alterné An. On construit une suite σk pour k variant de 1 à n - 2 tel que φσ1σ2...σn-2 soit égal à l'identité. On remarque alors que σn-2-1...σ2-1σ1-1 est un produit de cycles d'ordre 3 égal à φ. On raisonne par récurrence, si φ(1) est égal à 1 alors σ1 est l'identité, sinon, σ1 est le cycle (1φ-1(1)x1), où x1 est un entier compris entre 2 et n et différent de φ-1(1). On a φσ1(1) = φφ-1(1) = 1.
- On suppose, par hypothèse de récurrence, que φσ1σ2...σj-1 laisse invariant les entiers compris entre 1 et j - 1 et on construit un cycle σj tel que φσ1σ2...σj laisse invariant les entiers compris entre 1 et j. Ici, j désigne un entier inférieur à n - 2. Si φ(j) est égal à j, σj est l'identité sinon σj = (j (φσ1σ2...σj-1)-1(j) xj), ici xj désigne un entier différent de (φσ1σ2...σj-1)-1(j) et strictement supérieur à j, qui existe nécessairement. Comme, par hypothèse de récurrence, la restriction de φσ1σ2...σj-1 aux entiers compris entre 1 et j - 1 est l'identité, φσ1σ2...σj-1(j) est plus grand que j - 1 et σj laisse aussi invariant les j - 1 premiers entiers. Un calcul analogue à celui de σ1(1) montre que la restriction aux entiers compris entre 1 et j de φσ1σ2...σj est l'identité.
- La permutation φσ1σ2...σn-2 est un produit de permutations paires, elle est donc paire. La construction des σk montre que φσ1σ2...σn-2, est soit la transposition (n n-1), soit l'identité. Comme une transposition est impaire, la permutation est bien l'identité, ce qui termine la démonstration.
Exemples
La seule classe de conjugaison de S4 qui se trouve divisé en deux dans A4 est celle des cycles d'ordre 3. Un tel élément est en effet composé de deux cycles de longueurs impaires et différentes : 1 et 3. Les cycles d'ordre 1 sont en effet comptés. La classe de l'élément neutre ne contient qu'un élément et n'est jamais divisé. Celle composée de deux transpositions à supports disjoints n'est pas divisé en deux, elle contient des cycles de longueurs paires et contient aussi deux cycles de même longueur. On obtient 4 classes de conjugaison : l'identité, les produits de 2 cycles disjoints d'ordre 2 et deux classes de cycles d'ordre 3 :
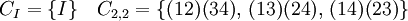
et
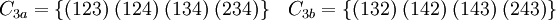
Dans le cas de A5, il est plus long d'écrire toutes les classes en extension, on trouve en effet 60 éléments. Il existe 5 classes de conjugaison. Une contient l'identité, une autre 15 permutations formées de deux transpositions à supports disjoints. Cette classe n'est pas divisée car elle contient un cycle de longueur paire. Les 20 cycles d'ordre 3 ne forment plus qu'une classe de conjugaison. Ils sont maintenant complétés par deux cycles de même longueur, ceux d'ordre 1. Enfin, les cycles d'ordre 5 sont divisés en 2 classes de conjugaisons contenant 12 permutations chacune.

















































